Определение угла между прямой и плоскостью
ТеорияОпределение угла между прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми, сводится к нахождению угла между двумя прямыми.
Чертежи на рис. 281 подтверждают это высказывание. Известно, что углом между прямой и плоскостью называется угол между этой прямой и ее прямоугольной проекцией на данную плоскость *.
* Естественно, речь идет о случае, когда прямая не перпендикулярна плоскости.

Геометрическая интерпретация приведенного определения показана на рис. 281,а. План решения задачи может быть записан в следующем виде:
1. Из произвольной точки К ∈ m опускаем перпендикуляр на плоскость α.
2. Определяем точку встречи зтого перпендикуляра с плоскостью - Кα (точка Кα - ортогональная проекция К на плоскость α) .
3. Находим точку А - пересечения прямой m с плоскостью α.
4. Проводим (КαА) - проекцию прямой m на плоскость α.
5. Угол ∠КАКα - искомый.
Решение этой задачи может быть значительно упрощено, если определять не угол между прямой и плоскостью (∠φ°), а дополнительный до 90° ∠ ψ°. В этом случае отпадает необходимость в определении точки Кα и проекции mα. Зная величину 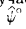 , вычисляем
, вычисляем  = 90° -
= 90° - 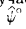
ПРИМЕР 1. Определить угол между прямой а и плоскостью α (m || n) (рис. 282) .
РЕШЕНИЕ.
1. Определяем направление горизонтальной проекции горизонтали h' и фронтальной проекции фронталн f" плоскости α.
2. Из произвольной точки К прямой а проводим прямую l ⊥ α; для этого через К' проводим l' ⊥ h' и через К" - l" ⊥ f".
3. Определяем величину угла ψ° вращением его вокруг горизонтали до положения, параллельного плоскости π1 .
Вычисляем значение искомого угла  = 90° -
= 90° - 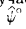
Решение аналогичной задачи упрощается, если плоскость задана следами, так как в этом случае отпадает необходимость в определении проекций линий уровня.

ПРИМЕР 2. Определить угол между прямой а и плоскостью α, заданной следами (рис. 283).
РЕШЕНИЕ
1. Из произвольной точки К прямой а опускаем перпендикуляр l на плоскость α(l' ⊥ h0α, l" ⊥ f0α )
2. Определяем величину угла ψ°.
3. Вычисляем значение искомого угла  = 90° -
= 90° - 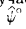 .
.