Определение точек пересечения линии с поверхностью

В общем случае для графического решения задачи по определению положения точек пересечения (встречи) линий с поверхностью необходимо выполнить ряд геометрических построений в приведенной ниже последовательности: заключить данную линию во вспомогательную поверхность; определить линию пересечения этой вспомогательной поверхности с заданной поверхностью; отметить точки, в которых пересекаются полученная линия с заданной (рис. 238).

* Эта теорема известна также как "теорема Монжа", по имени основоположника начертательной геометрии Гаспара Монжа, доказавшего эту теорему.

Запишем указанную последовательность решения в виде табл. 9 (как это сделано в § 43 при составлении алгоритма для решения задачи по определению линии пересечения двух поверхностей). В правой части таблицы приведена символическая запись, соответствующая смысловому содержанию отмеченных этапов решения.

Таблица 9

Алгоритм для решения задачи определения точек пересечения линии с поверхностью в символической форме можно записать:

{K,...} = (γ ∩ α) ∩ a.

Здесь, как и у алгоритма определения линии пересечения двух поверхностей, в зависимости от порядка и взаимного расположения заданных кривой и поверхности множество искомых точек {К, ...} может состоять из одной, двух и более точек.

Полученный алгоритм является универсальным, пригодным для решения задачи с любым вариантом задания исходных данных. Рассмотрим различные варианты решения задачи:

1. Пересечение кривой с поверхностью.

2. Пересечение кривой с плоскостью.

3. Пересечение прямой с поверхностью.

4. Пересечение прямой с плоскостью.

При решении всех этих задач, как правило, целесообразно для уменьшения графических построений и их упрощения пользоваться в качестве вспомогательной секущей поверхности γ - проецирующей цилиндричес-

кой поверхностью, в частности, если определяется точка пересечения прямой с поверхностью, - плоскостью. Упрощение решения достигается благодаря тому, что одна из проекций линии пересечения l автоматически определяется положением и формой следа проецирующей поверхности γ. Поэтому задача по определению точек встречи линии с поверхностью сводится к построению второй проекции линии, принадлежащей поверхности, если известна одна ее проекция, т. е. к задаче, которую мы неоднократно решали.

1. Пересечение кривой с поверхностью.

При определении содержания и последовательности выполнения геометрических операций, входящих в состав алгоритма для решения задачи по определению точек пересечения кривой с поверхностью, мы пользовались наглядным чертежом, изображенным на рис. 238. Теперь проследим, как решается эта задача на эпюре Монжа.

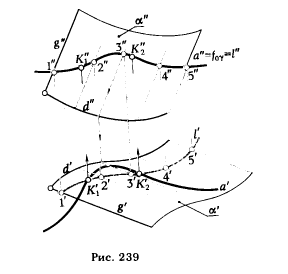
ПРИМЕР. Определить точки пересечения кривой а с произвольной цилиндрической поверхностью α (рис. 239) .

РЕШЕНИЕ.

1. Заключаем кривую а во фронтально проецирующую цилиндрическую поверхность γ.

2. Определяем линию пересечения поверхностей γ и α. Для этого отмечаем на а" ≡ f_0γ ≡ l" произвольные точки 1", 2", 3", 4", 5"; зная фронтальные проекции точек, находим их горизонтальные проекции 1', 2', 3', 4', 5'. Соединив эти точки плавной кривой, получим горизонтальную проекцию l' кривой l, по которой вспомогательная цилиндрическая поверхность γ пересекает данную поверхность α.

3. Отмечаем точки К'₁ и К'₂ пересечения кривых l' и а'. По горизонтальным проекциям определяем их фронтальные проекции К"₁ и К"₂.

2. Пересечение кривой с плоскостью.

Решение этой задачи аналогично только что рассмотренной, если и есть какое-либо отличие, то оно состоит лишь в том, что приходится определять вторую проекцию линии, принадлежащую не цилиндрической поверхности, как это было в приведенном выше примере, а плоскости.

ПРИМЕР. Определить точку встречи линии а с плоскостью α (рис. 240).

РЕШЕНИЕ.

1. Заключаем линию а в проецирующую цилиндрическую поверхность γ, безразлично какую γ ⊥ π₁ или γ ⊥ π₂ (на рис. 240γ ⊥ π )

2. Обозначим линию пересечения γ ∩ α = l, тогда l" ⊂ f_0γ.

3. Определяем горизонтальную проекцию Для этого отмечаем на l" ряд точек 1", 2", 3", ..., с помощью горизонталей (h₁, h₂, h₃, ...) плоскости α находим точки 1', 2 , 3',.... принадлежащие l'

4. Отмечаем точку К' = l' ∩ α', по К' находим К".

3. Пересечение прямой с поверхностью.

В алгоритме решения задачи для определения точек встречи прямой с поверхностью в качестве вспомогательной секущей поверхности следует брать плоскость.

Сложность решения рассматриваемой группы задач зависит от трудоемкости нахождения линии пересечения γ ∩ α, которая определяется видом поверхности α и расположением прямой а как относительно поверхности α, так и по отношению к плоскостям проекций.

Чтобы получить рациональное решение, следует пользоваться наиболее простым способом определения линии l(l = γ ∩ α). Этого можно достигнуть двумя путями: 1) соответствующим выбором положения вспомогательной секущей плоскости γ или 2) переводом секущей прямой а в частное положение. Рассмотрим каждый из этих вариантов решения.

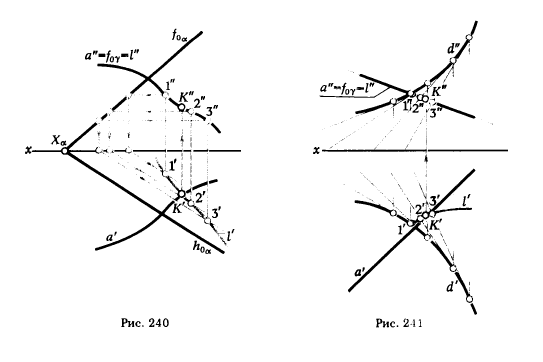
Вариант 1. а) Вспомогательная секущая плоскость - проецирующая.

ПРИМЕР. Определить точку пересечения прямой а с поверхностью торса (рис. 241).

РЕШЕНИЕ. Заключаем прямую а во фронтально проецирующую плоскость γ. Фронтальная проекция линии пересечения l" совпадает с f_0γ ≡ а". Отмечаем точку 1", в которой проекция l" пересекает проекцию d" ребра возврата d. Зная положение 1", определяем горизонтальную проекцию 1'. Проводим ряд прямолинейных образующих торсовой поверхности (касательных к кривой d) и фиксируем точки 2", 3", в которых l" пересекает фронтальные проекции этих образующих.

На горизонтальных проекциях соответствующих образующих определяем горизонтальные проекции 2', 3'. Соединив эти точки плавной кривой, получим горизонтальную проекцию l'.l' ∩ а' = К'- горизонтальная проекция искомой точки встречи. По К' определяем К".

б) Вспомогательная секущая плоскость - общего положения.

Использование вспомогательной проецирующей плоскости не всегда упрощает решение, возможны случаи, когда целесообразно применять плоскость общего положения.

В качестве иллюстрации, подтверждающей эту мысль, может служить задача по определению точек пересечения прямой общего положения с конической поверхностью.

Плоскость пересекает коническую поверхность по кривой. Исключение составляет только плоскость, проходящая через вершину кони-

ческой поверхности. В этом случае кривая второго порядка распадается на две прямые - образующие конической поверхности (см. § 45) *

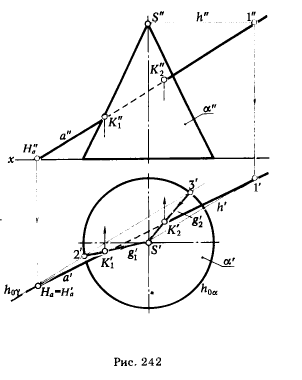
ПРИМЕР. Определить точки пересечения прямой а с поверхностью прямого кругового конуса α (рис. 242).

РЕШЕНИЕ. Заключаем прямую а в плоскость γ, проходящую через вершину конической поверхности S. На рис. 242 плоскость γ задана пересекающимися прямыми а и h , при этом h - горизонталь.

Определяем горизонтальный след плоскости γ; для этого находим горизонтальный след прямой Н_a и через него проводим h_0γ параллельно горизонтальной проекции горизонтали h'. Отмечаем точки 2' и 3', в которых h_0γ ∩ h_0α. (S'2') и (S'3') - образующие поверхности α, по которым она пересекается плоскостью γ.

Точки К'₁ и К'₂ (К'₁ = а' ∩ (S'2') и К'₂ = а' ∩ (S'3')) - горизонтальные проекции искомых точек пересечения. Зная положение К'₁ и К'₂, определяем К"₁ и К"₂.

Вариант 2. Перевод секущей прямой в частное положение.

При пересечении поверхности сферы плоскостью в сечении получается окружность, которая проецируется на плоскости проекции в общем случае в виде эллипсов или прямой и эллипса (если секущая плоскость проецирующая). В частном случае, когда секущая плоскость параллельна плоскости проекции, окружность проецируется на эту плоскость проекции без искажения. Поэтому, чтобы упростить решение задачи, следует произвольно расположенную прямую перевести в положение, параллельное какой-либо плоскости проекции. Тогда представляется возможность заключить прямую в плоскость, параллельную плоскости проекции.

ПРИМЕР 1. Определить точки встречи прямой а, заданной отрезком [АВ] с поверхностью сферы α (рис. 243).

РЕШЕНИЕ. Переводим прямую, произвольно расположенную в пространстве, в положение, параллельное плоскости проекции. Для этого переходим от системы xπ₂/π₁ к системе x₁π₃/π₁ в которой π₃ || а .

В этом случае горизонтально проецирующая плоскость γ ⊃ a пересечет поверхность сферы по окружности с радиуса R (см. рис. 243) , которая спроецируется на плоскость π₁ в [ 1'2'], а на плоскость π₃ в окружность с"₁ того же радиуса R. Точки K"₁ и К"₂ пересечения с"₁ с [А"₁В"₁] - вспомогательные проекции искомых точек, по ним определяем вначале К'₁ и К'₂, а затем и К"₁ и К"₂.

Если прямая а , пересекающая поверхность вращения, проходит через ось i этой поверхности, то перевод прямой а в частное положение целесообразно осуществить путем вращения прямой вокруг оси i.

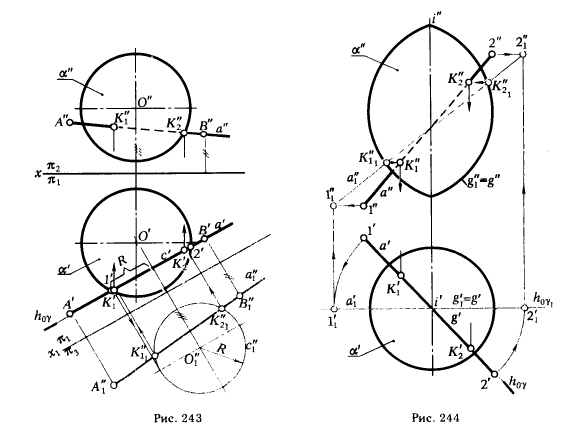
ПРИМЕР 2. Определить точки встречи прямой а с поверхностью вращения α (рис. 244).

* Если секущая плоскость проходит через вершину конической поверхности и составляет с ее осью угол больший, чем угол наклона к этой оси образующей конической поверхности, то сечение распадается на две мнимые прямые.

РЕШЕНИЕ. Горизонтально проецирующая плоскость γ, в которую заключаем прямую а , пересечет поверхность вращения по меридиану g₁.

Чтобы не строить искаженной фронтальной проекции меридионального сечения, поворачиваем плоскость γ и находящуюся в ней прямую а вокруг оси i до положения, параллельного π₂, тогда g'₁ совпадает g' - горизонтальной проекцией главного меридиана, a h_0γ с h_0γ1. После поворота прямая а займет положение a₁(а'₁, а"₁). С помощью точек К"₁₁ и К"₁₂ , в которых a"₁ ∩ g"₁, определяем положение К"₁ и К"₂, а затем К'₁ и К'₂.

4. Пересечение прямой с плоскостью.

Определение точки встречи прямой с плоскостью относится к элементарной задаче, но ее значение для решения самых различных, более сложных задач, трудно переоценить. Задача по нахождению точки встречи прямой с плоскостью входит как составная часть (фрагмент) в алгоритм решения широкого круга как позиционных, так и метрических задач.

Решение этой задачи даже в самом общем случае, когда и плоскость и прямая занимают произвольное положение в пространстве, легко сводится к простейшей задаче по определению линии пересечения двух плоскостей, из которых одна - проецирующая (см. § 44, рис. 187, 188), с последующим определением второй проекции точки, принадлежащей плоскости, если известна одна из ее проекций (см. § 40, примеры 1 ... 3, рис. 169... ...171). Для этого достаточно прямую заключить во вспомогательную проецирующую плоскость.

ПРИМЕР 1. Определить точку встречи прямой а с плоскостью α (рис. 245).

РЕШЕНИЕ. Так как а - прямая, то в алгоритме К = (γ ∩ α) ∩ a в качестве

секущей поверхности следует выбирать плоскость. Эта плоскость пересечет заданную α по прямой l . Поэтому в рассматриваемом случае предписываемая алго-

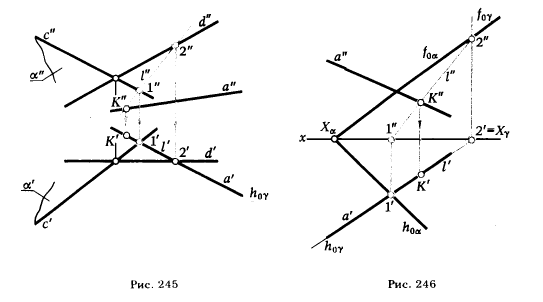
ритмом последовательность выполнения геометрических построений будет иметь следующее содержание:

1) проводим через а' (или а") горизонтальный (фронтальный) след горизонтально проецирующей (фронтально проецирующей) плоскости γ;

2) определяем фронтальную (горизонтальную) проекцию линии пересечения плоскости γ с данной плоскостью α l" = γ" ∩ α" (или l' = γ' ∩ α');

3) определяем К" = а" ∩ l" (или К' = а' ∩ l'); зная К", находим К' (или зная К', находим К").

Алгоритм решения не меняется, если мы будем иметь дело с другим вариантом задания плоскости - параллельными прямыми или прямыми, по которым плоскость пересекает плоскости проекций (следами плоскости).

ПРИМЕР 2. Определить точку пересечения прямой а с плоскостью α (рис. 246).

РЕШЕНИЕ. Так же, как и в предыдущем примере, заключаем прямую а в проецирующую плоскость γ ⊃ a (h _0γ ≡ а'). Строим линию пересечения плоскостей γ ∩ α = l . Отмечаем К" = l" ∩ α". По К" находим К'.

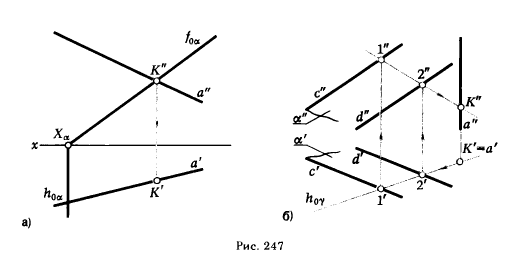
Решение задачи упрощается, если одна из заданных фигур (прямая или плоскость) занимает проецирующее положение. Рис. 247,а и б иллюстрирует решение таких задач:

а) плоскость α - проецирующая, а прямая a -общего положения (рис. 247 а);

б) плоскость α - общего положения, а прямая а - проецирующая (рис. 247,6).

Решения задач настолько просты, что они ясны из чертежей и не требуют каких-либо пояснений.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Изложите общий принцип построения обобщенного алгоритма для решения задачи по определению линии пересечения поверхностей.
2. Сформулируйте возможные варианты решения задачи по определению линии пересечения многогранника плоскостью.
3. В каких случаях для определения линии пересечения двух поверхностей можно применять способ:

а) вращающихся плоскостей;

б) пучка плоскостей с несобственной прямой;

в) концентрических сфер;

г) эксцентрических сфер?

4. Какие точки линии пересечения поверхностей называются опорными?
5. Напишите и дайте пояснение алгоритма решения задачи по определению точки встречи прямой с плоскостью.
6. В чем заключается решение задач по определению сечения поверхности плоскостью с помощью способа граней и способа ребер?
7. В каких случаях плоскость пересекает поверхность прямого кругового конуса: по двум пересекающимся прямым, по окружности, эллипсу, параболе, гиперболе?
8. Что представляют собой фронтальные проекции линии пересечения двух поверхностей вращения второго порядка, имеющих общую плоскость симметрии, параллельную плоскости π₂ ?
9. Какая зависимость существует между порядком пересекающихся поверхностей и порядком линии, полученной в результате их пересечения?
10. Сформулируйте условия (теоремы) , при которых кривая - линия пересечения поверхностей - распадается на две кривые второго порядка?
11. Приведите примеры, когда кривая - линия пересечения двух цилиндрических поверхностей - распадается на одну, две, три, четыре прямых.
12. В чем состоит содержание алгоритма решения задачи для определения точек пересечения линии с поверхностью?
13. Чем следует руководствоваться при выборе вспомогательной секущей поверхности при определении точек пересечения линии с поверхностью?
14. В каком случае можно для упрощения решения задачи по определению точек встречи прямой с поверхностью применять способ вращения вокруг оси, перпендикулярной плоскости проекции?