Определение угла между плоскостями
ТеорияМерой угла между двумя плоскостями служит линейный угол, образованный двумя прямыми - сечениями граней этого угла плоскостью, перпендикулярной к их ребру.
Для построения линейного угла, являющегося мерой двугранного угла, необходимо выполнить следующие геометрические построения:
1. Определить прямую а - линию пересечения данных плоскостей α и β, а = α ∩ β (рис. 284).
2. Провести плоскость γ (γ ⊥ α и γ ⊥ β).
3. Построить прямые m = γ ∩ α и n = γ ∩ β.
4. Найти величину угла  между прямыми m и n. Угол
между прямыми m и n. Угол  - искомый.
- искомый.
Рассмотренный план решения задачи предусматривает выполнение большого числа геометрических построений, связанных с нахождением линии пересечения данных плоскостей (а = α ∩ β), проведением плоскости, перпендикулярной к найденной прямой (γ ⊥ а ). Далее приходится еще дважды решать задачу по определению линии пересечения плоскостей (m = γ ∩ α и n = γ ⊥ β) и лишь только после этого можно приступить к определению величины искомого угла  .
.
Проследим, как можно упростить решение этой задачи. Дополним чертеж на рис. 284 точкой К ∈ γ и опустим из этой точки перпендикуляры k и l на плоскости α и β (рис. 285). Точки М и N пересечения
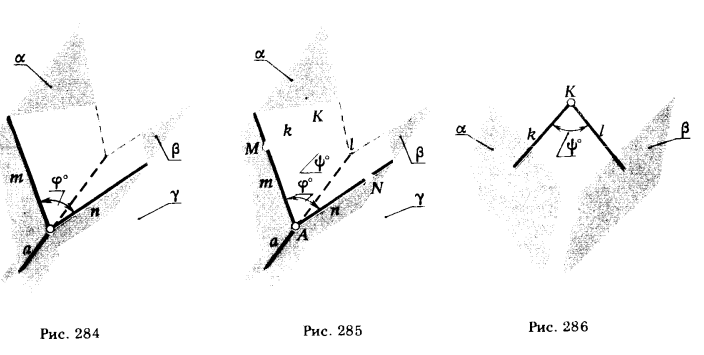
этих перпендикуляров с плоскостями совместно с точками К и А (А ∈ а ) являются вершинами плоского четырехугольника KNAM, у которого углы при вершинах М и N прямые. Следовательно, между углами при вершинах А и К существует зависимость, которую можно выразить следующим равенством:  = 180° - ψ°. Из рис. 285 видно, что вместо ∠ψ° гораздо проще определять дополнительный до 180° ∠ψ°. Все решение сводится к построению угла ψ° путем проведения из произвольной точки пространства К прямых k и l, перпендикулярных к заданным плоскостям, и определению угла ψ° между этими прямыми; после чего подсчитывается значение величины
= 180° - ψ°. Из рис. 285 видно, что вместо ∠ψ° гораздо проще определять дополнительный до 180° ∠ψ°. Все решение сводится к построению угла ψ° путем проведения из произвольной точки пространства К прямых k и l, перпендикулярных к заданным плоскостям, и определению угла ψ° между этими прямыми; после чего подсчитывается значение величины  = 180° -
= 180° - 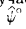 (рис. 286).
(рис. 286).
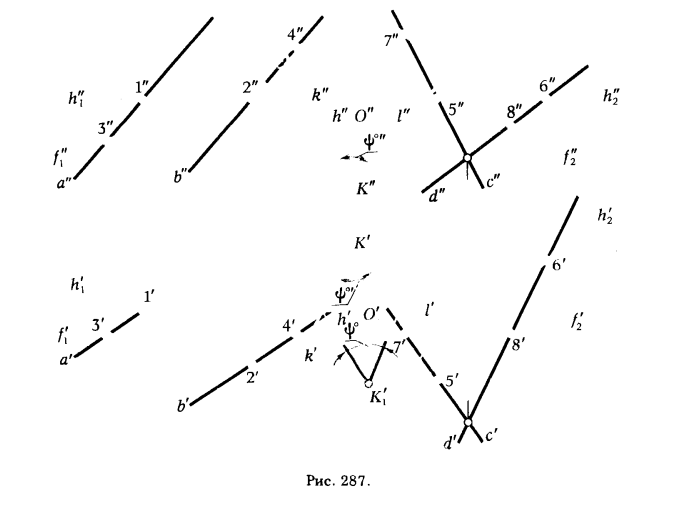
ПРИМЕР 1. Определить угол между плоскостями α(а || b) и β(с ∩ d) (рис. 287).
РЕШЕНИЕ.
1. Определяем направление горизонтальных проекций горизонталей h'1 и h'2, фронтальных проекций фронталей f"1 и f"2 заданных плоскостей α и β.
2. Из произвольной точки К проводим проекции перпендикуляров k и l (k' ⊥ h'1, k" ⊥ f"1 и l' ⊥ h'2, l" ⊥ f"2).
3. Определяем величину 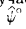 .
.
4. Вычисляем значение  = 180° -
= 180° - 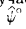 .
.
Если плоскости, угол между которыми требуется определить, задан следами, то решение упрощается еще больше, так как отпадает необходимость в выполнении п.1 только что рассмотренного решения.
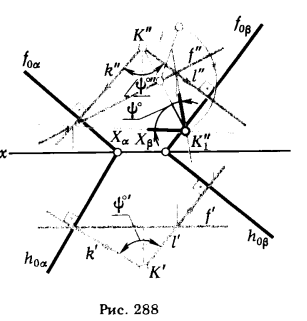
ПРИМЕР 2. Определить угол между плоскостями α и β, заданными следами (рис. 288)
РЕШЕНИЕ. Все геометрические построения сводятся к проведению через точку К прямых, перпендикулярных к следам плоскостей α и β (k' ⊥ h0α, k" ⊥ f0α и l' ⊥ h0β, l" ⊥ f0β). Затем известным способомнаходим величину  (на рис. 288 угол
(на рис. 288 угол 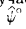 определен путем вращения вокруг фронтали). Зная
определен путем вращения вокруг фронтали). Зная 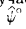 , вычисляем значение
, вычисляем значение  .
.