Определение величины плоского угла по его ортогональным проекциям

В предыдущем параграфе было отмечено, что плоский угол проецируется на плоскость проекции без искажения в том случае, когда его стороны параллельны этой плоскости. Это свойство может быть принято за основу при составлении алгоритма решения задачи на определение величины угла по его искаженным ортогональным проекциям.

Решение задачи будет сводиться к перемещению плоскости общего положения, которой принадлежит угол, в положение, параллельное какой-либо плоскости проекции. Такое перемещение можно осуществить с помощью способов преобразования ортогональных проекций.

Наиболее рациональное решение задачи по переводу плоскости угла в положение, параллельное плоскости проекции, достигается путем вращения плоскости угла вокруг линии уровня. В этом случае для получения ответа на поставленную задачу достаточно произвести поворот только одной точки вокруг горизонтали или фронтали плоскости угла - построить только одну вспомогательную проекцию.

При использовании других способов преобразования нам пришлось бы дважды менять плоскости проекции, либо дважды осуществлять перемещение (или вращение), параллельное плоскости проекции, т. е. в обоих случаях потребовалось бы построение двух вспомогательных проекций.

Приведенные ниже примеры иллюстрируют использование способа вращения вокруг линии уровня для решения задачи по определению величины плоского угла.

ПРИМЕР 1. Определить угол между пересекающимися прямыми а и b (рис. 279).

РЕШЕНИЕ. Вращаем плоскость α, определяемую прямыми а и b, вокруг ее горизонтали h до нового положения, параллельного плоскости π₁. Точки А и В принадлежат оси вращения h , поэтому при вращении плоскости α вокруг оси h они не меняют своего положения. Следо-

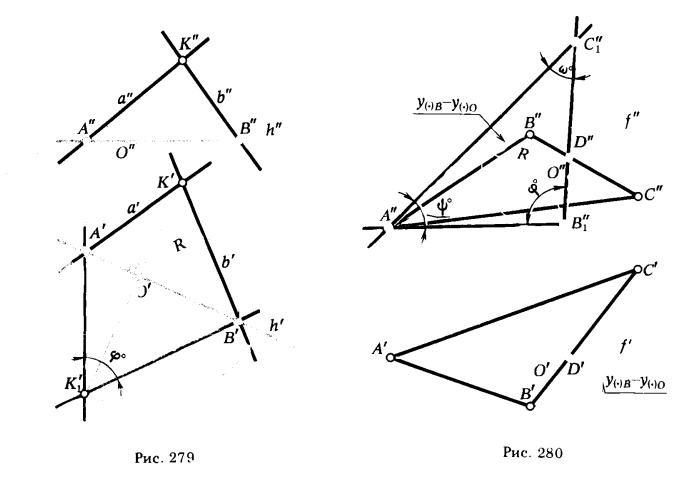
вательно, для определения нового положения плоскости α₁ достаточно осуществить поворот только одной точки К. Для этого проводим через К' прямую, перпендикулярную h' (с этой прямой будет совпадать горизонтальная проекция окружности, по которой перемещается точка при ее вращении вокруг h ). Далее определяем положение центра вращения О и величину радиуса вращения R для точки К (построения выполнены аналогично тому, как это было сделано на рис. 71, § 11). Положение точки К'₁ совместно с А' и В' определяет новые проекции прямых a'₁ и b'₁, задающих плоскость α₁.Поэтому А'К'₁В' равен искомому углу φ°.

ПРИМЕР 2. Определить величину углов ΔАВС (рис. 280) .

РЕШЕНИЕ. Вращаем плоскость ΔАВС вокруг фронтали f этого треугольника до положения, параллельного плоскости π₂. Через вершину А ΔАВС проводим фронталь f(f', f"). Точки А и D как принадлежащие оси вращения не изменят своего положения в процессе преобразования. Поэтому, как и в предыдущем примере, достаточно повернуть только одну точку. На рис. 280 в качестве такой точки взята вершина В ΔАВС.

Вершина треугольника С при вращении вокруг фронтали будет перемещаться по дуге окружности, плоскость которой перпендикулярна оси вращения f; поэтому фронтальная проекция этой окружности перпендикулярна f" и новое положение С"₁ определится в точке пересечения этого перпендикуляра с новым положением прямой B"₁D". После такого поворота плоскость треугольника переводится в положение, параллельное плоскости π₂. Следовательно, на основании инвариантного свойства 2д (см. § 6) углы при вершинах А", В"₁ и С"₁ проецируются без искажения.