Определение расстояния между точкой и прямой, между параллельными прямыми
ТеорияРасстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.
Это определение может быть положено в основу составления алгоритма графического решения задачи определения расстояния от точки до прямой.
Рис. 263 дает наглядное представление о графическом решении задачи по определению расстояния от точки А до прямой а . Через точку А можно провести множество прямых {l1, l2,l3, ..., ln} , перпендикулярных к прямой а . Это множество прямых определяет плоскость γ. Чтобы выделить из {l1, l2,l3, ..., ln} единственную прямую lj, пересекающую прямую а , необходимо найти точку встречи прямой а с плоскостью γ - М = а ∩ γ; определить длину отрезка [AM].
Реализация этого алгоритма путем геометрических построений значительно упрощается, если прямая будет параллельна плоскости проекции.
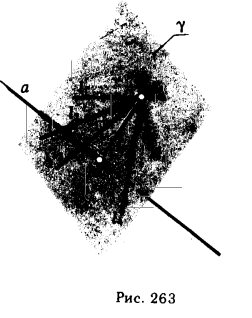
В этом случае можно без каких-либо вспомогательных построений провести проекции прямой, перпендикулярной данной и проходящей через заданную точку. На рис. 264 показано решение такой задачи. Как видно из чертежа, решение достигается минимальным числом геометрических построений. Поэтому нет смысла решать эту задачу в общем виде, а следует предварительно с помощью способов преобразования ортогональных проекций перевести прямую в положение, параллельное плоскости проекции (см. рис. 260, 261,262).
Решение задачи на определение расстояния между параллельными прямыми ничем не отличается от только что рассмотренного примера. Это утверждение базируется на том, что расстояние между параллельными прямыми определяется величиной перпендикуляра, опущенного из точки, взятой на одной прямой, на другую прямую.
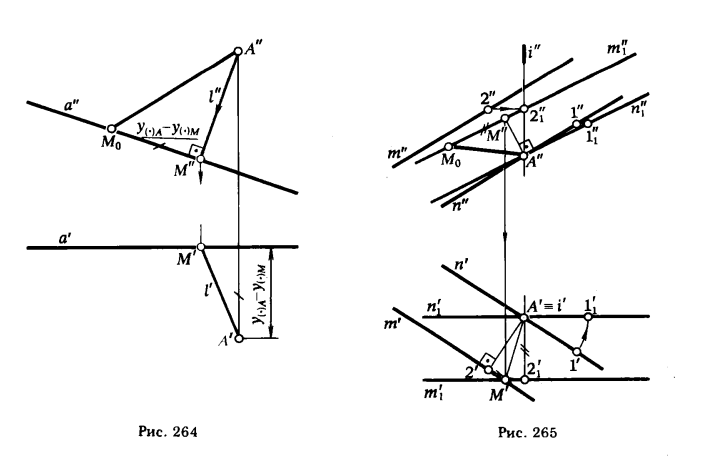
ПРИМЕР I. Определить расстояние между пераллельными прямыми m и n (рис. 26В) .
РЕШЕНИЕ. На прямой n отмечаем произвольную точку A ∈ n . Вращаем прямые m и n вокруг оси i (i ∋ A, i ⊥ π1 ) до положения m1|| π2 и n1 || π2. Из точки A" опускаем перпендикуляр А"М" на прямую m"1. Определяем действительную величину [AM] .
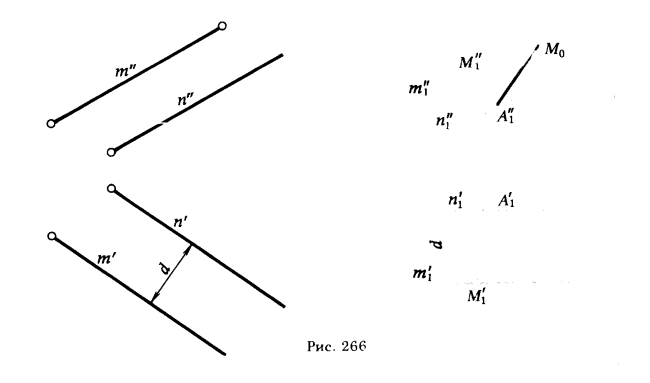
На рис. 266 показан второй вариант решения этой задачи. С помощью способа параллельного перемещения прямые тип переведены в положение, параллельное плоскости π2. Дальнейшее решение сводится к определению расстояния от точки А, взятой на одной прямой, до другой прямой m1.
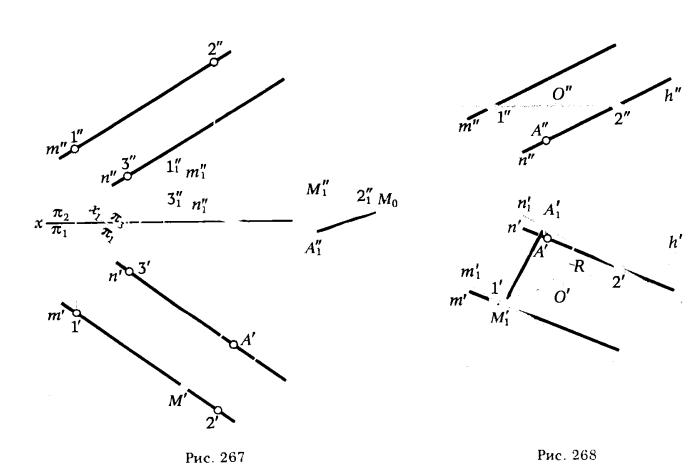
Перевод прямых m и n из общего положения в частное можно осуществить путем замены плоскости π2 новой плоскостью π3, параллельной прямым m и n. Решение задачи этим способом приведено на рис. 267.
На рис. 268 рассматриваемая задача решена путем вращения прямых m и n вокруг горизонтали h до положения, параллельного плоскости π1.