Определение величины углов

171*. Определить углы наклона прямой АВ к пл. V и пл. Н фис. 166, а).

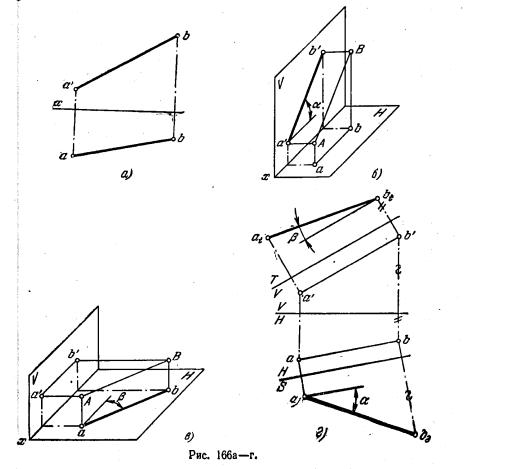
Решение. Если прямая параллельна пл. V (рис. 166, б), то угол между этой прямой и пл. H (угол α) изображается без искажения на фронт. проекции. Если же прямая параллельна пл. H (рис. 166, в), то образуемый зтой прямой угол с пл. V (угол β) изображается без искажения на горизонт. проекции. Поэтому, поставив заданную прямую общего положения сначала параллельно пл. V, а затем параллельно пл. H, можно определить соответственно углы α и β.

На рис. 166, г показано применение способа перемены пл. проекций для определения углов α и β. Так, для определения угла α введена дополнительная пл. S, перпендикулярная к пл. H и параллельная АВ, а для определения угла β — дополнительная плоскость Т ⊥ V и в то же время || АВ.

На рис. 166, д прямая как бы повернута: а) вокруг оси, проходящей через точку В и перпендикулярной к пл. H, до параллельности пл. V (положение а'₁b' , а₁b) —

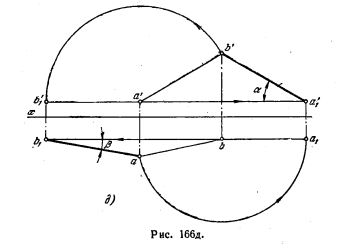
определен угол α; б) вокруг оси, проходящей через точку А перпендикулярно и пл. V, до параллельности пл. H (положение a'b'₁, ab₁) — определен угол β.

Конечно, можно изобразить эти оси на чертеже; но, как видно, построение возможно и без этого.

172. Дана пирамида SABCD (см. рис. 154). Определить углы наклона ребер пирамиды к пл. V и пл. Н.

173*. Определить углы наклона плоскости, заданной треугольникам ABC (рис. 167, а), к пл. Н и пл. V.

Решение. Как известно, угол наклона (α) плоскости к пл. H проецируется без искажения на пл. V, если плоскость перпендикулярна к пл. V (рис. 167, 6), а угол наклона (β) плоскости к пл. V проецируется без искажения на пл. H, если плоскость перпендикулярна к пл. H (рис. 167, в).

На рис. 167, г для определения углаос переходим к системе S, H, где пл. S перпендикулярна к пл. H и к заданной плоскости (ось S/Н перпендикулярна к горизонт. проекции а—1 горизонтали).

Определение угла β произведено путем перехода от системы V, Н к системе Т, V, где пл. Т перпендикулярна к пл. V и к данной плоскости треугольника (ось T/V перпендикулярна к фронт. проекции с'2' фронтали).

На рис. 167,д та же задача решена способом параллельного перемещения. Сначала все вершины заданного треугольника ABC перемещены в плоскостях, параллельных H, так, чтобы плоскость треугольника оказалась перпендикулярной к пл. V. Это

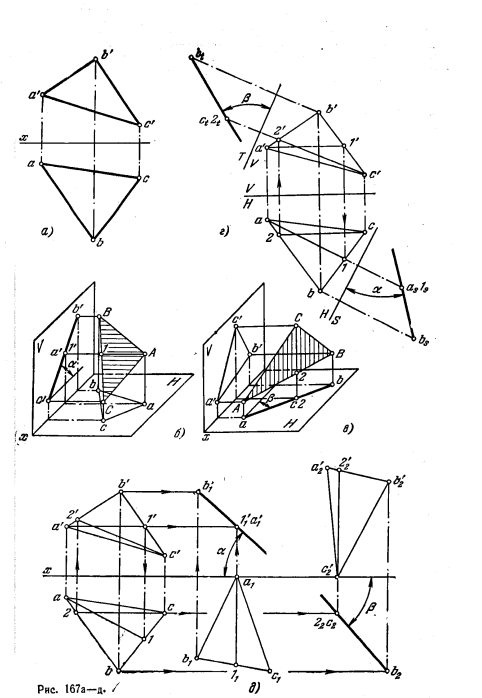
достигнуто с помощью горизонтали А—1, перемещенной так, что она расположилась перпендикулярно к пл. V (горизонт. проекция а₁1₁ перпендикулярна к оси х). Получаем угол α наклона плоскости треугольника к пл. H без искажения.

Для определения величины угла β наклона плоскости треугольника ABC к пл. V треугольник повернут так, чтобы он расположился перпендикулярно к пл. H. Это сделано при помощи фронтали С—2: она поставлена перпендикулярно к пл. H (положение C₂2₂, фронт. проекция с'₂2'₂ ⊥ х) и, следовательно, проходящая через эту фронтвль плоскость также перпендикулярна к пл. H.

174. Дана пирамида SABC (см. рис. 161). Определить углы наклона граней SAB, SAC и ABC к пл. H и пл. V.

175. Дан параллелепипед (см. рис. 165). Определить углы наклона основания ABCD и грани CDHG к пл. V и грани ADEH к пл. Н.

176*. Определить величину угла ВАС (рис. 168, а).

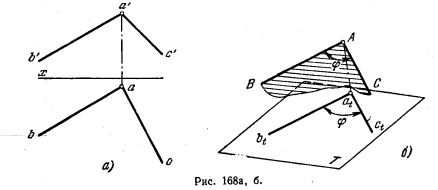
Решение. Если плоскость угла параллельна какой-либо пл. проекций, то данный угол проецируется на нее без искажения (рис. 168, б).

На рис. 168, в задача решена при помощи способа перемены пл. проекций. Так как плоскость угла ВАС является плоскостью общего положения (ее горизонталь не перпендикулярна ни к одной из плоскостей V, Н, W), то приходится сначала дополнить систему V, H пл. S, взяв ее перпендикулярно к пл. H и к плоскости угла ВАС. В результате этого преобразования проекция угла на плоскости S получится в виде отрезка a_s l_s. Теперь можно ввести еще одну дополнительную пл. проекций (T), проведя ее перпендикулярно к пл. S и в то же время параллельно плоскости угла ВAС. Угол l_ta_t2_t представит собою натуральную величину угла ВАС.

На рис. 168, а искомый угол ср определен способом параллельного перемещения.

Сначала плоскость угла перемещена так, чтобы она стала перпендикулярной к пл. V (для этого располагаем горизонт. проекцию горизонтали перпендикулярно к оси х). Затем располагаем плоскость угла параллельно пл. H, для чего перемещаем проекцию 1'₁a'₁ в положение 1'₂a'₂ (т. е. || оси х). Еще одно построение показано на рис. 168,6. Здсь для определения величины угла применен поворот вокруг горизонтали: плоскость угла расположится параллельно пл. H (положение Т).

Построения выполнены в следующем порядке:

1. Проведена плоскость вращения точки А — горизонтально-проецирующая пл. R, перпендикулярная к горизонтали (т. е. к оси вращения).

2. Отмечен центр вращения точки АВ пересечении горизонтали с пл. R (точка О, О') и указаны проекции радиусАВращения (Оа и О'а').

3. Определена натуральная величина радиуса вращения (ее выражает гипотенуза ОА треугольника ОаА).

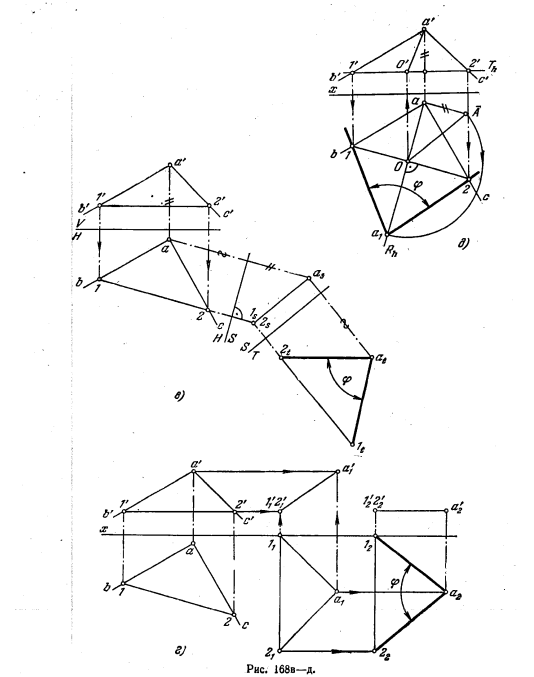
4. Проведена дуга окружности радиуса ОА я на R_h, найдена точка a₁- горизонт. проекция вершины угла после его поворота вокруг горизонтали до совмещения с пл. Т — и построен угол 1а₁2, равный искомому.

Для решения задач типа 176 наиболее рациональным является применение вращения вокруг горизонтали (или фронтали), как это показано на рис. 168, д.

177. Дана пирамида SABC (см. рис. 156). Вращением вокруг горизонтали определить угол между ребрами и SB, SB и SC, SC и SA.

178. Дан параллелепипед (см. рис. 165). Определить углы между ребрами DH и CD, CG и CD, АВ и ВС.

179*. Определить величину угла между скрещивающимися прямыми АВ и CD (рис. 169, а).

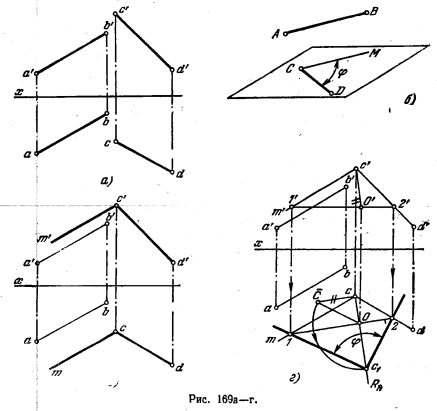
Решение. Угол между двумя скрещивающимися прямыми определяется углом, доставленным пересекающимися прямыми, соответственно параллельными данным скрещивающимся. Для определения величины угла надо начать с его изображения нр чертеже. Это сделано на рис. 169,6, причем использована одна из заданных прямых - CD, через точку С которой проведена прямая СМ, параллельная другой заданнай прямой—АВ. Величина угла MCD (рнс.169, в) выражает угол между прямыми АВ и CD. Это сделано при помощи поворота вокруг горизонтали 1—2 (рис. 169, а), взятой в пл. угла MCD.

180. Дана пирамида SABC (см. рис. 160). Определить величину угла между ее ребрами: a) SB и АС, б) SA и ВС.

181*. Определить величину угла φ наклона прямой АВ к плоскости, заданной треугольником CDE (рис. 170, а).

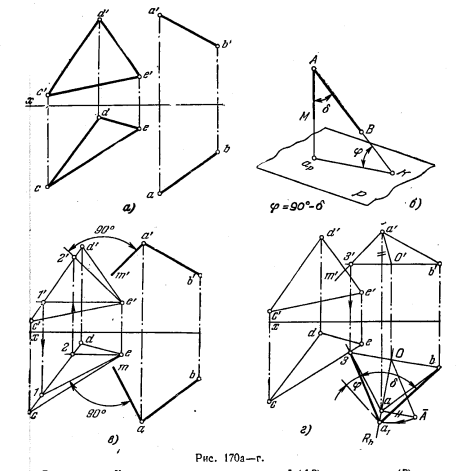
Решение. Как известно, углом между прямой (АВ) и плоскостью (Р) называется острый угол (φ) между прямой и ее проекцией (а_pК) на этой плоскости. Для построения (рис. 170, б) этого угла надо найти точки пересечения с пл. Р прямой АВ и перпендикуляра, проведенного из какой-либо точки прямой АВ на пл. Р. Но если, как в данной задаче, требуется лишь определить величину угла наклона прямой к плоскости, то проще определить величину угла δ, дополнительного к углу φ: найдя угол δ, можно определить величину угла φ из соотношения φ = 90° — δ. На рис. 170, в показано построение проекций am и а'm' перпендикуляра к плоскости треугольника CDE, для чего взяты горизонталь цфронталь этой плоскости: am ⊥ e — 1, а'm' ⊥ е'2'.

Теперь можно определить (рис. 170,г) натуральную величину угла δ с вершиной А,- что сделано поворотом вокруг горизонтали b'З', b—3. Искомый угол φ = 90°—δ.

182. Дана пирамида SABC (см. рис. 1611. Определить углы наклона ребер SA, SB и SC к грани AВС

183*. Определить угол между гранями АBС и ABD (рис. 171, а).

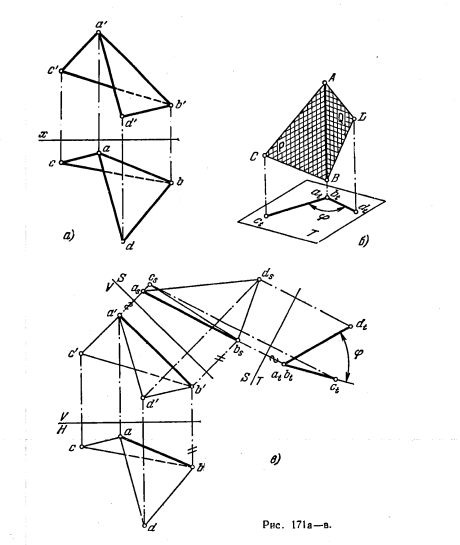
Решение. Двугранный угол измеряется линейным углом, полученным в пересечении граней двугранного угла плоскостью, перпендикулярной к обеим граням двугранного,а следовательно, и к линии их пересечения, т. е. ребру двугранного угла. Если это ребро АВ окажется перпендикулярным к какой-либо пл. Т (рис. 171,6), то полученная на пл. Т проекция двугранного угла выражает его линейный угол.

Для решения задачи (рис. 171, в) применен способ перемены пл. проекций. Oт системы V, H совершен переход к системе S, V, где S ⊥ V и S || АВ, а затем от этой системы S, V переход к системе Т, S, где T ⊥ S и Т ⊥ AB.

Треугольники проецируются на пл.Т в виде отрезков а_tc_t и а_td_t. Угол между ними равен искомому углу φ.

На рис. 171, г показано решение той же задачи при помощи способа параллельного перемещения: ребро АВ поставлено перпендикулярно к пл. Н.

184*. Определить величину угла, образованного плоскостью Р и плоскостью треугольника ABC (рис. 172, а).

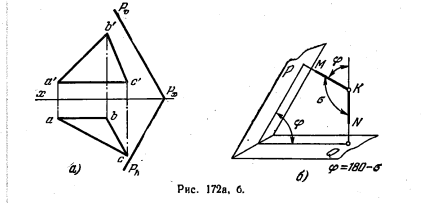
Решение. Если, решая данную задачу, придерживаться схемы решения предыдущей, то необходимо построить прямую пересечения заданных плоскостей. Но можно поступить и иначе, без построения этой прямой, т. е. не определяя ребра искомого двугранного угла. Можно поступить следующим образом: определить не непосредственно угол φ, а угол σ (рис. 172, б) между перпендикулярами КМ и KN, проведенными из какой-либо точки К на заданные плоскости. Найдя угол σ, получаем φ = 180° — σ.

Такое решение отличается в своей сущности от решений по рис. 171, в и 171, а. Взяв некоторую точку К (рис. 172, в), проведем из нее перпендикуляры КN и КМ соответственно к плоскости треугольника ABC н к пл. Р: из точки k' проводим k'n' ⊥ a'b' и k'm' ⊥ P_ϑ, а из точки k — kn ⊥ ac и km ⊥ P_h. Таким образом получается угол с проекциями mkn и n'k'n' (угол σ) .Натуральная величина этого угла получена поворотом вркруг фронтали 1—2 (рис. 172, г). Так как получен острый угол, то можно

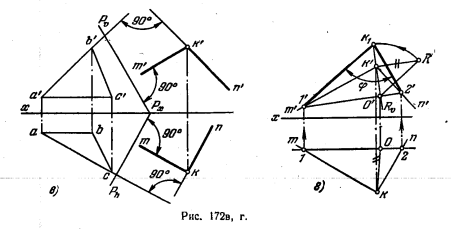
считать, что он определяет искомый угол между заданными плоскостями, так как из смежных углов, полученных при взаимном пересечении двух плоскостей, углом между плоскостями считается острый.

185. Дана пирамида SABCD (см. рис. 154). Определить способом перемены плоскостей проекций углы между гранями SAB и SBC, SBC и SCD, SAD и SAB.

186. Дан параллелепипед (рис. 165). Определить углы между гранями CDHG и EFGH, BCGF и CDHG.