Пересечение прямой линии с плоскостью общего положения
ТеорияДля построения точки пересечения прямой с плоскостью общего положения надо выполнить следующее (рис. 158):
1)через данную прямую (АВ) провести некоторую вспомогательную плоскость (α),
2) построить прямую (МN) пересечения плоскости данной (β) и вспомогательной (α),
3)определить положепие точки (К) пересечения прямых — данной (АВ) и построенной (МN).
На рис. 172 показано построение точки пересечения прямой FK с плоскостью общего положения, заданной двумя пересекающимися прямыми АВ и CD.

Через прямую FK проведена вспомогательная фронтально-проецирующая плоскость β. Выбор фронтально-проецирующей плоскости объясняется удобством построения точек пересечения ее фронтального следа с проекциями А"В" и C"D". По точкам М" и N" найдены горизонтальные проекции М' и N' и тем самым определена прямая MN, по которой вспомогательная пл. β пересекает данную пл. α. Затем найдена точка К', в которой горизонтальная проекция прямой непосредственно или при своем продолжении пересекает проекцию M'N'. После этого остается найти фронтальную проекцию точки пересечения — точку К".
На рис. 173 показано построение точки пересечения прямой MN с плоскостью, заданной треугольником АВС. Ход построения не отличается от рассмотренного на рис. 172. Но вспомогательная (на этот раз горизонтально-проецирующая) плоскость в данном случае указана только одним следом γ', проходящим через проекцию M'N'. Пл. γ пересекает АВС по прямой DE. Но можно обойтись и без γ': мысленно представляя себе вспомогательную горизонтально-проецирующую плоскость, проходящую через MN, выражаем проекциями E'D' и E"D" отрезок ED, по которому проведенная через MN горизонтально-проецирующая плоскость пересекает треугольник.
Считая, что в пространстве заданы прямая и непрозрачный треугольник, определим видимые и невидимые части прямой MN относительно плоскостей π1 и π2.
В точке Е' на пл. π1, совмещаются горизонтальные проекции двух точек, из которых одна принадлежит прямой MN (фронтальная проекция E"1), а другая — стороне треугольника АС (фронтальная проекция Е").
Из расположения фронтальных проекций E"1 и Е" следует, что на участке КМ прямая находится над треугольником и, следовательно, на горизонтальной проекции отрезок М'К' — весь видимый, а отрезок K'D' — невидимый.
На фронтальной проекции в точке F" совмещаются фронтальные проекции двух точек, из которых одна принадлежит прямой MN, а другая — стороне треугольника АВ. По расположению горизонтальных проекций F' и F'1 заключаем, что прямая MN на участке МК находится за треугольником и, следовательно, на фронтальной проекции отрезок F"K" — невидимый, а отрезок K"N" — видимый.
На рис. 174— 176 даны примеры построения точки пересечения прямой с плоскостью общего положения, выраженной следами. В первом примере через прямую АВ проведена горизонтально-проецирующая пл. β, а во втором (рис. 175) — горизонгальная плоскость, что оказалось возможным сделать, так как в этом примере прямая АВ — горизонгальная.
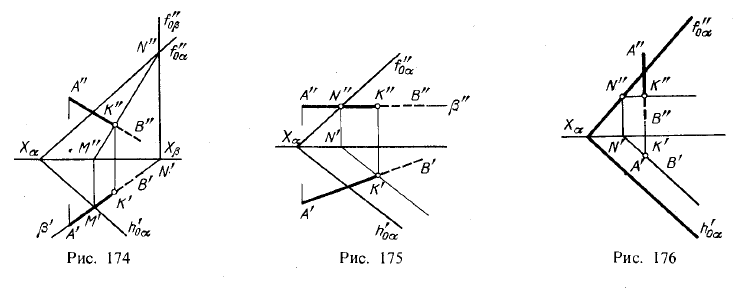
Изображенная на рис. 176 прямая перпендикулярна к пл. π1 Горизонтальные проекции всех точек этой прямой сливаются в одну точку. Следовательно, положение проекции К' искомой точки пересечения прямой АВ с пл.α известно. Положение проекции К" определено при помощи горизонтали.