Примеры решения задач с применением способов перемены плоскостей проекций и вращения

1. Построить проекции точки пересечения двух профильных прямых, лежащих в общей для них профильной плоскости.

Решение дано на рис. 204. Применен способ перемены плоскостей проекций. Для получения проекции К" надо отложить отрезок К"2, равный найденному отрезку К'"1.

2. Провести дополнительную плоскость проекций так, чтобы прямая общего положения оказалась перпендикулярной к этой плоскости.

Решение дано на рис. 209. Введены последовательно две дополнительные плоскости проекций. Отрезок АВ расположен перпендикулярно ко второй дополнительной пл. пр. π₄

3. Повернуть прямую общего положения так, чтобы она стала перпендикулярной к пл. π₁.

Решение дано на рис. 222. Применены два поворота. После второго поворота отрезок АВ перпендикулярен к пл. π₁.

4. Определить длину отрезка прямой общего положения и углы ее наклона к плоскостям проекций π₁ и π₂.

На рис. 202 показано решение способом перемены плоскостей проекций. Введена дополнительная пл. π₃1⊥π₂, параллельная данному отрезку CD. Определены длина отрезка и угол с пл. π₂.

На рис. 219 показано решение способом вращения. Выполнен поворот вокруг оси, проведенной через точку А отрезка АВ, который выведен в положение, параллельное пл. π₂. Определены длина отрезка и угол с пл. π₁.

5. Определить расстояние от точки до прямой.

Обратимся к рис. 228. На нем показан поворот плоскости, определяемой точкой К и прямой АВ, вокруг горизонтали KD этой плоскости. В результате поворота плоскость располагается параллельно пл. π₁. Теперь (рис. 235) можно провести перпендикуляр K'L': отрезок К'L' определяет искомое расстояние от точки К до прямой АВ.



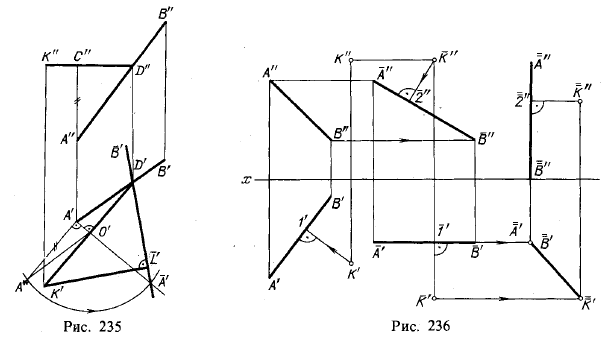
На рис. 236 показано решение той же задачи вращением системы, состоящей из точки К и прямой АВ, вокруг осей — сначала перпендикулярной к пл. π₁ ( затем перпендикулярной к пл.π₂. Оси не изображаются (см. § 36). Так как при первом повороте горизонтальная проекция системы только меняет свое положение, но не конфигурацию и величину, то, проведя перпендикуляр К'1', строим горизонтальную проекцию A'B' в требуемом положении. По этой проекции находим фронтальную проекцию A"B"2"K". При втором повороте надо сохранить конфигурацию и величину этой проекции. «Привязываем» точку K" к A"B" при помощи перпендикуляра K"2" и строим проекцию A"B"2"K", а по ней проекцию K' точки К и точку с двойным обозначением (A' и B') — проекцию отрезка АВ. Искомое расстояние от точки К до прямой АВ выражается отрезком K'A' (K'B').

6. Определить расстояние от точки до плоскости.

На рис. 201 показано решение для случая горизонтально-проецирующей плоскости. Решение сводится к проведению перпендикуляра А'К'.

На рис. 237 показано решение для случая плоскости общего положения; слева плоскость задана треугольником, справа — следами. Применен способ перемены плоскостей проекций — введена дополнительная пл. π₃, перпендикулярная к пл. π₁, и к данной плоскости, которая в результате оказывается перпендикулярной к пл. π₃ (см. рис. 205 и 206 и пояснения к ним). Искомое расстояние определяется перпендикуляром, проведенным из точки К'" к проекции В"'С"' (рис. 237, слева) и к следу α"' (рис. 237, справа).

7. Определить расстояние между двумя параллельными плоскостями.

Решение этой задачи можно свести к определению расстояния от точки, взятой в одной из плоскостей, до другой плоскости или ввести в систему π₁ π₂ дополнительную плоскость проекций, перпендикулярную к данным параллельным плоскостям, как это сделано на рис. 237 в отношении одной плоскости.


8. Определить расстояние между двумя параллельными прямыми.

Решение этой задачи можно свести к определению расстояния от точки, взятой на одной из прямых, до другой прямой (см, рис, 235 и 236),

На рис. 238 показано построение, при котором плоскость, определяемая параллельными прямыми, повернута вокруг одной из ее горизонталей (или фронталей) так, что плоскость, а следовательно, и данные прямые расположились параллельно плоскости проекций.

Вращение произведено вокруг горизонтали КМ. Достаточно найти новое положение хотя бы точки А (на горизонтальной плоскости точка A'): прямая A''К' и параллельная ей прямая, проведенная через точку М', представляют собой горизонтальные проекции данных параллельных прямых, когда плоскость, ими определяемая, расположена параллельно пл. π₁.

На рис. 239 показано решение той же задачи способом перемены плоскостей проекций. Сначала обе прямые спроецированы на пл. π₃, им параллельную (пл. π₃ проведена через одну из прямых — через АВ). Затем прямые спроецированы на пл. π₄, к ним перпендикулярную. На ней проекции прямых являются точками. Отрезок A^IVC^IV (или B^IVD^IV) определяет искомое расстояние между прямыми..

На том же рис. 239 показаны проекции отрезка, определяющего расстояние между данными прямыми. Проекция на пл. π₃ проведена через точку В"' (можно было бы взять и какую-либо другую точку на А'"В"') параллельно оси π₃/π₄, так как в системе π₃, π₄ проекция на пл. π₄ выражает натуральную величину расстояния между АВ и CD. Дальнейшее ясно из чертежа. Проекция на пл. π₄ должна быть больше каждой из проекций В"'Е"', В'Е', В"Е".

9. Определить кратчайшее расстояние между скрещивающимися прямыми и выразить в проекциях общий к ним перпендикуляр. Напомним, что кратчайшее расстояние между двумя скрещивающимися прямыми есть в то же время и расстояние между параллельными плоскостями, в которых лежат скрещивающиеся прямые.

На рис. 240 показан общий перпендикуляр к скрещивающимся прямым АВ и CD.

Если через АВ и CD провести параллельные между собой плоскости α и β, затем через одну из этих прямых, хотя бы через АВ, провести пл. δ, перпендикулярную к α и β, и найти прямую пересечения плоскостей δ и β (эта прямая MN параллельна прямой АВ), то в точке Е пересечения прямых CD и MN будет проходить искомый перпендикуляр к прямым АВ и CD.

В построении, показанном на рис. 241, одна из скрещивающихся прямых (АВ) спроецирована в точку на дополнительную плоскость проекций (π₄). Выполнен следующий план построения:

а) От системы π₁, π₂ перейти к системе π₃, π₁, где π₃⊥π₁ и π₃ || АВ.

б) От системы π₃, π₁ перейти к системе π₃, π₄, где π₄⊥π₃ и π₄⊥ АВ.

в)Получив на плоскости проекций π₄ проекцию прямой АВ в виде точки и проекцию второй прямой C^IVD^IV и проведя из A^IV (B^IV) перпендикуляр на C^IVD^IV, найти искомое расстояние между данными скрещивающимися прямыми АВ и CD.

Далее, на рис. 241 показано построение проекций общего для АВ и CD перпендикуляра. Ход построения указан стрелками. Проекция E"'F"' проведена параллельно оси π₃/π₄.

10. Построить проекции отрезка прямой общего положения, составляющей с пл. π₁ угол φ₁, а с ПЛ; π₂ угол φ₂. Такое построение было уже показано в § 13 (рис. 73 и 74), но без применения способов, изложенных в главе V. Теперь рассмотрим решение при помощи способа вращения.

Пусть (рИс. 242) прямая должна пройти через точку А под углом φ₁ к пл. π₁ и под углом φ₂ к пл. π₂. Известно (см. § 13), что для прямой общего положения φ₁ + φ₂ < 90°.

Через точку А проведены две прямые: одна параллельно пл. π₂ под углом φ₁, к π₁ другая параллельно пл. π₁ под углом φ₂ к π₂. На обеих прямых отложены равные отрезки: А"B" = А'B'. Повернем отрезок АB вокруг оси, перпендикулярной к π₁ а отрезок АB вокруг оси, перпендикулярной к π₂, причем обе эти оси проходят через точку А (что позволяет сохранить эту точку в заданном ее положении). В некоторый момент оба отрезка совпадут



(на рис. 242 это показано в виде отрезка А В), и, следовательно, окажется построенной искомая прямая. Всего можно провести через точку А четыре такие прямые.


11. Построить плоскость общего положения, проходящую через точку А и расположенную под заданными углами к пл. π₁ и к пл. π₂.

На с. 77 была установлена зависимость между углами, составляемыми плоскостью общего положения с пл. π₁ и с пл. π₂, и углами, составляемыми перпендикуляром к этой плоскости с теми же плоскостями проекций. На основании этих зависимостей для построения плоскости под углами σ₁ к π₁ σ₂ к π₂ надо предварительно построить прямую под углами φ₁ = 90° — σ₁, к π₁ и φ₂ = 90° — σ₂ к π₂ (см. задачу 10), а затем через заданную точку А провести плоскость, перпендикулярную к построенной прямой ¹).

12. Плоскость общего положения, заданную треугольником АВС (рис. 243), повернуть вокруг заданной вертикальной оси так, чтобы эта плоскость прошла через заданную точку К. Если плоскость пройдет через точку К, то эта точка окажется в плоскости на одной из ее горизонталей. Можно сразу указать ту горизонталь, которая после поворота плоскости должна пройти через точку К: для этого достаточно провести фронтальную проекцию горизонтали через точку К". Построив горизонтальную проекцию горизонтали (M'N') и определив радиус вращения (O'D'), проводим окружность, по отношению к которой горизонтальная проекция горизонтали будет касательной в любом положении при вращении плоскости вокруг данной оси. Если теперь провести из точки К' касательную к этой окружности (K'D'), то мы можем принять ее за горизонтальную проекцию горизонтали, на которой должна находиться точка К, когда плоскость пройдет через нее.

Построив горизонтальную проекцию горизонтали после поворота (M'N'), строим горизонтальную проекцию треугольника: она лишь меняет положение, но остается неизменной по виду и величине (A'B'C' = А'В'С'). По проекции A'B'C' находим проекцию A"B"C".

Ограничиваемся одним решением. Второе решение получится, если провести из точки К' вторую касательную.

Только что рассмотренная задача может быть видоизменена следующим образом: повернуть плоскость общего положения вокруг некоторой вертикальной оси так, чтобы данная точка оказалась в этой плоскости.

Эта задача отличается от предыдущей только тем, что ось вращения нам надо выбрать самим. Можно ли выбрать ее произвольно?

Оказывается, что не каждая из прямых, перпендикулярных к плоскости π₁ может быть принята в качестве оси, пригодной для решения данной задачи.

Из рис. 243 следует, что горизонтальная проекция оси вращения должна быть расположена так, чтобы относительно горизонтальных проекций точки К и горизонтали MN окружность с центром О', касающаяся прямой M'N', не заключала внутри себя точки К', так как из точки К' приходится проводить касательную к этой окружности.

Значит, расстояние искомой точки О' от точки К' должно быть во всяком случае не меньше, чем расстояние этой же точки О' от прямой M'N'. Если мы возьмем точку О' так, чтобы оба эти расстояния были равны (например, в точке O₁ или 0₂ на рис. 244), то в ней еще можно установить ось вращения.



Где на чертеже будут лежать все такие точки, которые одинаково удалены и от точки К, и от прямой M'N'? Известно, что они располагаются на кривой линии — параболе, фокус которой находится в точке К, а директрисой служит прямая M'N'. Точки, находящиеся внутри этой параболы, лежат ближе к фокусу, чем к директрисе, и непригодны в качестве горизонтальной проекции оси вращения; точки же на самой параболе или вне ее могут быть выбраны в качестве такой проекции.

¹) Очевидно, построив прямую и так, как было показано в § 13, мы можем провести к ней перпендикулярную плоскость, которая и будет искомой.

13. Через точку, лежащую в некоторой плоскости, провести в этой плоскости прямую под заданным углом φ₁ к пл. π₁.

Положим, что плоскость (назовем ее α) задана двумя пересекающимися прямыми (рис. 245, слева) и что надо провести искомую прямую через точку А, в которой эти прямые пересекаются.

Найдем горизонтальный след пл. α. Для этого проведена ось проекций х и найдены горизонтальные следы обеих прямых, определяющих пл. α. Через эти следы проходит след h'_0α. Если бы искомая прямая АВ была параллельна пл. π₂, то угол между проекцией А"В" и осью проекций равнялся бы углу между прямой и пл. π₁. Поэтому через точку А" (рис. 245, справа) надо провести прямую под заданным углом φ₁ к оси проекций.



Точку В" на этой прямой можно взять произвольно; она взята для простоты на оси х. Затем построена горизонтальная проекция А'В', соответствующая полученному отрезку А"В". Проекция А'В' должна быть параллельна оси проекций, так как прямая поставлена параллельно пл. π₂.

Построенная прямая (А"В", А'В') удовлетворяет одному условию: она проведена под заданным углом (φ₁ к пл. π₁ но не удовлетворяет другому: она не лежит в заданной плоскости. Чтобы ввести прямую АВ в пл. α и в то же время сохранить угол φ₁ неизменным, надо повернуть ее вокруг оси вращения, перпендикулярной к пл. π₁. Так как точка А лежит в пл. α, то надо взять ось вращения, проходящую через точку А (рис. 246); точка В при этом вращении будет двигаться в пл. π₁ и в тот момент, когда АВ войдет в пл. α, точка В будет на h'_0α этой плоскости. Поэтому, вращая прямую А'В' вокруг точки О'(А'), «выводим» точку В' на след h'_0α и по найденному новому положению горизонтальной проекции находим новое положение проекции на пл. π₂.

Задача, как видно из рис. 246, имеет два ответа, и решение ее возможно, если заданный угол φ₁ не больше угла наклона самой пл. α к пл. π₁. Если эти углы равны между собой, то получается только один ответ.

14. Найти натуральную величину плоского угла.

Решение этой задачи можно видеть на рис. 203 и 210, где построение выполнено с помощью способа перемены плоскостей проекций (треугольник спроецирован на параллельную ему дополнительную плоскость проекций, и тем самым определены углы треугольника). Затем можно увидеть определение натуральной величины плоского угла с помощью способа вращения на рис. 223 и 227, а также на рис. 230 и 234, где при совмещении плоскости с соответствующей плоскостью проекций найдена натуральная величина угла между следами плоскости в первой четверти.

15. Разделить плоский угол Пополам. Вопрос о построении на чертеже биссектрисы угла был затронут в § 15: рассматривались те случаи задания угла, когда Проведение биссектрисы угла проекции соответствовало делению пополам угла в пространстве. Теперь рассматривается общий случай. Решение показано на рис. 247.

Плоскость, определяемую сторонами заданного угла, следует расположить параллельно одной из плоскостей проекций; тогда угол изобразится в своей проекции на этой плоскости без искажения и может быть разделен пополам. На рис. 247 плоскость угла повернута до положения, параллельного пл. π₁. Для выполнения этого проведена горизонталь АС. Поворот треугольника АВС вокруг горизонтали АС сводится к повороту одной вершины — точки В. Центр вращения получается в точке О (проекция 0"0'); натуральная величина радиуса вращения R_B получается при построении прямоугольного треугольника О'В'В*, в котором катет О'В' представляет собой горизонтальную проекцию радиуса вращения, а катет В'В* равен отрезку В"1.

Точку B соединяют с точками А' и С — горизонтальными проекциями точек, расположенных на оси вращения и принадлежащих сторонам угла. Новую горизонтальную проекцию — угол А'BС', равный заданному углу АВС, делят пополам и получают при этом точку D' на горизонтальной проекции горизонтали, а затем и соответствующую ей проекцию D" на прямой А" С". Эти точки D' и D" представляют собой проекции точки, расположенной на оси вращения АС и, следовательно, «неподвижной». Прямые B"D" и B'D' являются проекциями искомой биссектрисы угла.

16. Найти натуральную величину угла между прямой линией и плоскостью.

На рис. 202 и 219 показано определение величины угла прямой общего положения с плоскостями проекций.

Теперь рассмотрим решение в случае некоторой плоскости общего положения.



Если требуется определить лишь величину угла между прямой и плоскостью, то построение проекций этого угла не является необходимым ¹). Действительно, величину угла между прямой АВ и пл. π₀ (рис. 248) можно определить, если построить угол φ₂ и определить его величину: искомый угол φ₁ = 90° — φ₂. Но при этом значительно упрощается решение задачи, так как отпадают все построениπ₁ связанные с нахождением точек D и А⁰.

Построение дано на рис. 249. Проводя из точки А прямой АВ перпендикуляр на пл. α, мы строим проекции угла, дополняющего искомый угол между прямой АВ и пл. α до 90°. Проводим горизонталь СВ и вращением вокруг нее располагаем плоскость, определяемую углрм САВ, параллельно пл. π₁. Новая горизонтальная проекция ∠C'AB' = ∠CAB. Теперь остается построить угол, дополняющий угол C'AB' до 90°; на рис. 249 это угол φ₁. Он равен искомому углу между прямой АВ и плоскостью.

Если плоскость задана не следами, а, например, треугольником, то надо для проведения к ней перпендикуляра построить в треугольнике горизонталь и фронталь (см. § 29).

17. Определить натуральную величину угла между двумя плоскостями.

На рис. 250 показано решение без построения проекций линейного угла, измеряющего двугранный, образуемый плоскостями α и β²). Такое решение особенно удобно, когда плоскости заданы следами.

Если из некоторой точки провести перпендикуляры к граням двугранного угла, то искомый линейный угол будет равен разности между углом 180° и углом, образованным этими перпендикулярами. На рис. 250 для определения угла между плоскостями α и β выполнены следующие построения:

а)из некоторой точки К проведены перпендикуляры: один к пл. α, другой к пл. β;

б) поворотом вокруг горизонтали угол, образованный перпендикулярами, расположен параллельно пл. π₁.

Искомый угол между плоскостями α и β равен найденному углу φ или (если φ — тупой угол) разности между углом 180° и найденным углом.

На рис. 251 дано решение с помощью способа перемены плоскостей проекций. Определена величина двугранного угла, образованного треугольными гранями АВС и ABD. Ребром служит отрезок АВ. Если АВ окажется перпендикулярным к дополнительной плоскости проекций, то обе грани спроецируются на нее в виде отрезков, угол между которыми равен линейному углу данного двугранного (рис. 252)

Построение на рис. 251 выполнено по следующей схеме: от системы π₁ π₂ к системе π₃, π₁ где π₃⊥π₁ и π₃|| АВ, и затем к системе π₃, π₄, где π₄⊥π₃ и π₄⊥АВ. На пл. π₃ показаны только проекции точек А, В, С и D; грани АВС и ABD не очерчены.



¹) О построении проекций угла между прямой и плоскостью см. § 31, с. 78.

²) О построении проекций линейного угла в двугранном см. § 31, с. 78.

Определение натуральной величины углов между плоскостью общего положения и плоскостями проекций π₁ и π₂ с помощью способа перемены плоскостей проекций было показано на рис. 205, 206 и 207, а на рис. 221 — с помощью способа вращения (угол, с пл. π₂).

18. Определить натуральный вид треугольника.

Решение с помощью способа перемены плоскостей проекций можно найти на рис. 203 и 210, а на рис. 223 и 227 — с помощью способа вращения.

19. Точку А повернуть вокруг оси MN на угол φ по часовой стрелке, если смотреть от М к N (рис. 253).

Построение выполнено с помощью способа перемены плоскостей проекций. Последовательным образованием новых систем плоскостей проекций по схеме: от системы π₁, π₂ к системе π₃, π₁, где π₃⊥π₁ и π₃ || MN, и, наконец, к системе π₃, π₄, где π₄⊥π₃ π₄⊥MN, получаем взаимно параллельное расположение плоскости вращения точки А и плоскости



проекций π₄. В связи с этим поворот точки А изображается как поворот проекции А^IV на заданный угол вокруг центра M^IV(N^IV) по часовой стрелке (так как, по условию для определения направления вращения, следует смотреть от точки М к точке N). Далее получаем проекцию А'" на прямой, проведенной через А'" перпендикулярно к M'"N'",а затем проекции А' и А", что соответствует перемещению точки А в положение А.

20. Построить проекции окружности заданного диаметра, расположенной в плоскости общего положения.

Решение дано на рис. 254. Для большей ясности построение выполнено поэтапно. Применен способ вращения.

Пусть плоскость (назовем ее α), в которой расположена: окружность, задана горизонталью с проекциями С"Н" и С'Н' и фронталью с проекциями C"F" и C'F'. Центр окружности — в точке С.

В первой позиции (рис. 254, слева) задаемся осью х и, найдя горизонтальный след фрон- тали CF - точку М, проводим след h'_0α параллельно проекции С'Н' горизонтали. Находим на пл. π₁ совмещенное положение центра С (точка C) и строим в пл. π₁ окружность заданного радиуса с центром в этой точке.

Искомые проекции окружности — эллипсы. На рис. 254 показано построение осей этих эллипсов для каждой проекции окружности.

Для эллипса, являющегося горизонтальной проекцией окружности, большая ось располагается на горизонтальной проекции горизонтали, причем (см. рис. 254, в середине) С'3'=С'4' = радиусу окружности, а малая ось получена при помощи диаметра 34, параллельного следу h'_0α, и диаметра 12, перпендикулярного к этому следу; точка 2' получена при помощи прямой 3К'₁, а точка 1' на той же проекции может быть построена на основании того, что С'2' = С'1'.

Справа на рис. 254 показано, что для фронтальной проекции большая ось 7"8" находится на фронтальной проекции фронтали; от точки С" отложены отрезки С"7" и С"8", равные радиусу окружности. Оси 7"8" соответствует диаметр 78 окружности, расположенной на совмещенной с π₁, фронтали MF.

Малая ось 5"6" на фронтальной проекции проведена перпендикулярно к 7"8". Точка 5" построена при помощи точки 5 диаметра 56 окружности, проведенного перпендикулярно к диаметру 78, продолженного до пересечения со следом h'_0α, в точке К'₃; на вспомогательной прямой С'К'₃ на горизонтальной проекции находим проекцию 5' и по ней строим точку 5". Откладывая отрезок С"6", равный отрезку С"5", получим проекцию малой оси 5"6".

Построив оси обоих эллипсов, можно перейти к построению самих эллипсов по точкам. Можно получить эти точки и так, как показано на рис. 254 (в середине) для точки А; построение проекций А' и А" аналогично указанному выше построению точек 5' и 5".

21. Построить фронтальную проекцию угла, натуральная величина которого равна его горизонтальной проекции.

В § 15 было установлено, что проекции острого (или тупого) угла, расположенного в плоскости общего положения могут равняться проецируемому углу.



Положим, что (рис. 255) угол А'К'В' — горизонтальная проекция некоторого угла φ. Проведя прямую А'В' — горизонтальный след плоскости, в которой лежит рассматриваемый угол, поворачиваем вокруг нее точку К до совмещения ее с пл. π₁. Если провести окружность через точки А', В' и К', то любой вписанный в нее угол, опирающийся на дугу А'С'В', равен φ, в том числе и угол А'KВ'. Очевидно, точка K является совмещенной с пл. π₁ точкой К — вершиной угла АКБ. Точка K получается в пересечении дуги, проведенной через точки А', В' и К', со следом h'_0β плоскости вращения точки К. Радиусом вращения точки К является отрезок О'K. Проведя перпендикуляр в точке К' к О'К' и засекая этот перпендикуляр дугой радиуса О'K, получаем точку К* и отрезок К'К*, представляющий собой расстояние точки К от пл. π₁ т. е. расстояние проекции К” от оси х. Угол А"К"В" представляет собой искомую фронтальную проекцию угла АКB, равного своей горизонтальной проекции А'К'В'.

В данном и некоторых предыдущих параграфах были рассмотрены задачи, в которых надо было определить общие элементы различных геометрических фигур (например, построение точки пересечения прямой линии с плоскостью или первая из задач в данном параграфе)

Для таких задач встречается название «позиционные». Им противопоставляются задачи, называемые метрическими, в которых определяются длины отрезков, углы, площади и др.

Вопросы к § 38

1. В какой последовательности взять оси вращения, чтобы поворотом вокруг них расположить прямую общего положения перпендикулярно к пл. π₁, к пл. π₂?
2. Как определить натуральную величину отрезка прямой общего положения и ее углы с пл. π₁ и с пл. π₂?
3. Как определить расстояние от точки до прямой общего положения?
4. Как определить расстояние от точки до плоскости общего положения, до профильной плоскости?
5. Как определить расстояние между двумя параллельными плоскостями, между двумя параллельными прямыми, между скрещивающимися прямыми?
6. Можно ли с помощью способа вращения построить проекции отрезка прямой общего положения по углам ее наклона к пл. π₁ и к пл. π₂? Если можно, то как это сделать?
7. Что обозначает парабола, построенная на рис. 244?
8. Как найти натуральную величину плоского угла?
9. Как построить на чертеже биссектрису угла?
10. Как найти натуральную величину угла между прямой линией и плоскостью?
11. Как найти натуральную величину угла, образованного двумя плоскостями?
12. Как построить проекции окружности, расположенной в плоскости общего положения?