Составление машинных алгоритмов решения задач

Простейший пример алгоритма — математическая формула, она указывает, над какими величинами и в какой последовательности необходимо выполнять арифметические операции для решения более сложных задач. Если при графическом методе процесс решения нельзя записать в виде формулы, то это можно сделать с помощью схемы счета, указывающей последовательность выполнения различных геометрических операций, реализуемых с помощью операторов, приведенных в табл. 10.

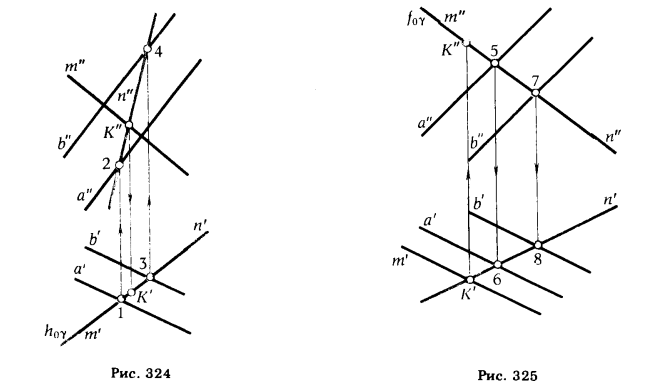
Установим алгоритм и запишем его в виде схемы счета, составленной из стандартных операторов для решения задачи по определению точки встречи прямой с плоскостью (рис. 324). Пусть заданы плоскость α (а || b) и пересекающая ее прямая m. Требуется найти точку К = m ∩ α.

Мы знаем, что для решения этой задачи необходимо прямую m заключить в плоскость γ; найти прямую пересечения плоскостей γ ∩ α = n; отметить проекцию точки К, в которой пересекаются одноименные проекции заданной прямой m и полученной линии пересечения n. Все необходимые построения приведены на рис. 324. Индексация арабскими цифрами указывает на последовательность определения точек.

В рассматриваемом случае схема счета, представляющая алгоритм решения задачи, записанный в символах стандартных операторов (табл. 10), примет вид

V₁III₂V₃V₄III₅V₆I₇V₈III₉V₁₀.

Выполнение двух операторов III_nV_n+1 можно заменить одним оператором VI_a *. Окончательно схема счета машинного алгоритма запишется

V₁ VI_a2 V₃ VI_a4 I_5- V₆ VI_a7.

(1)  (2)  (3)  (4)       (K') (K")                                    (5)

Арабские цифры и буквы в скобках указывают точку, обозначенную на чертеже, которая получается в результате выполнения оператора, под которым она поставлена.

Проследим, как будет изменяться схема счета, а следовательно, и алгоритм решения задачи в зависимости от взаимного расположения геометрических фигур как между собой, так и по отношению к плоскостям проекций.

Внесем изменение в эпюр, задающий исходные данные предыдущей задачи (см. рис. 324) так, чтобы горизонтальная проекция m' прямой m заняла положение, параллельное горизонтальным проекциям а' и Ь' прямых а и b (рис. 325).

В данном случае решить задачу так, как в предыдущем случае, не представляется возможным. Действительно, если мы заключим прямую m в горизонтально проецирующую плоскость γ, а затем будем определять с помощью оператора V точку 1, то сделать это нам не удастся, так как пересечение а" и b" произойдет в несобственной точке (а" ∩ b" = 1_∞). По той же причине нельзя определить и точку 3. Не имея точек 1 и 3, мы не получим точек 2 и 4, а следовательно, нам не удастся найти проекцию n" прямой n. Но эта задача может быть решена по схеме счета (5), если решение начать с фронтальных проекций (см. рис. 325).

* Такая замена целесообразна, так как она уменьшает затраты машинного времени. На выполнение двух операторов III, V требуется 26 команд, оператор VI_a реализуется с помощью только 11 команд.

Как следует из рис. 325, схема счета по формальным признакам ничем не отличается от предыдущей:

V  VI_a  V  VI_a  I  V  VI_a.

(5)  (6)  (7) (8)    (K') (K")                                    (6)

Условимся считать этот путь вторым вариантом решения в отличие от первого варианта, описанного схемой счета (5).

Когда одна из заданных геометрических фигур (прямая или плоскость) занимает проецирующее положение, решение задачи представляется следующими схемами счета:

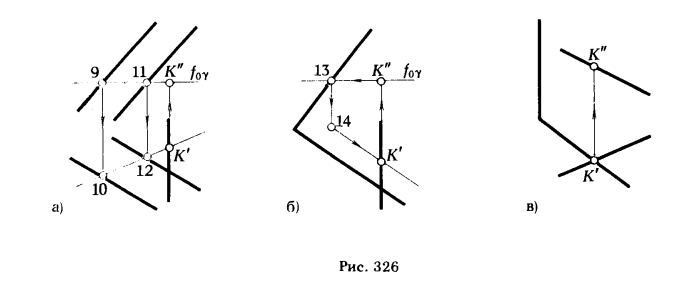
а) прямая — проецирующая, плоскость общего положения задана параллельными прямыми (рис. 326,а) :

VI_б VI_a VI_б VI_a I V VI_a;

(9) (10) (11) (12)    (K') (K")                                  (7)

б) прямая — проецирующая, плоскость общего положения задана следами (рис. 326,6) :

VI_б VI_a II V

(13)(14)   (K')               (8)

в) плоскость — проецирующая, прямая общего положения (рис. 326, в) :

V VI_a

(K')(K")               (9)

Все многообразие случаев задания исходных данных задачи по определению точки встречи прямой с плоскостью может быть отнесено к семи альтернативным вариантам. Кроме схем счета (5), (6), (7), (8), (9) отметим еще:

V VI_a   II   V VI_a

(15)(16)    (K")(K')             (10)

(рис. 327,а)

VI_б VI_a VI_б VI_a

(17)(18) (K")(K')             (11)

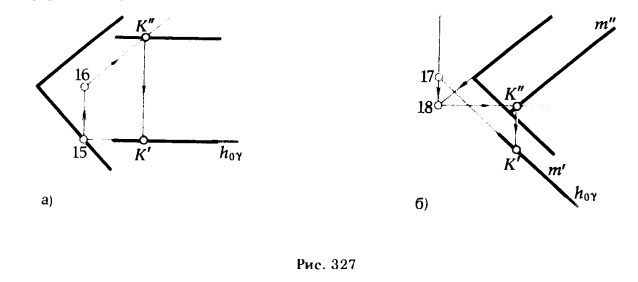
(рис. 327,6)

Приведенные примеры иллюстрируют изменение алгоритма решения одной и той же задачи в зависимости от характера расположения геометрических фигур.

Программирование решения многих задач является трудоемким процессом. Поэтому, чтобы каждый раз, когда машина приступает к решению задачи с другими исходными данными, не составлять новую программу (схему счета, которая является управляющей программой), следует создать единый (обобщенный) алгоритм, запрограммировав который получим программу, пригодную для решения всех вариантов данной задачи. Чтобы выяснить логическую схему построения обобщенного алгоритма, выпишем составленные ранее схемы счета частных алгоритмов в виде табл. 11.

Из табл. 11 (строка 1) видно, что если после выполнения оператора V₁ точка пересечения найдена, то следует переходить к выполнению оператора VI_a2, если и в этом случае точка определяется, то машина должна приступить к выполнению следующего оператора V₃ и т. д., пока не будет выполнен оператор VI_a7 , завершающий решение задачи.

Это решение соответствует исходным данным, показанным на рис. 324. Если при решении задачи по варианту I после выполнения оператора V₆ точку не получили (случай, изображенный на рис. 326,а), то следует переходить к выполнению группы операторов VI_б15 VI_a16 VI_a18 I₁₉ V₂₀ (табл. 11, строка 2). Если в результате выполнения оператора VI_б17 новой точки не будет, то следует переходить к выполнению операторов II₂₁ V₂₂ (табл. 11, строка 3, рис. 326,6).

Таблица 11

Отсутствие новой точки после выполнения оператора VI_a4 может служить указанием для перехода к выполнению операторов V₂₃ VI_a24 (табл. 11, строка 4, рис. 326,в). В том случае, когда не найдена новая точка после выполнения оператора V₃, переходят к выполнению группы операторов V₂₅ VI_a26 II₂₇ V₂₈ VII_a29 (табл. 11, строка 5, рис. 327,а).

Если при выполнении оператора V₁ точку не получили, переходят к выполнению варианта II решения (табл. 11, строка 6, рис. 325). И, наконец, если точку не получают при выполнении операторов V₁ и V₈, то необходимо переходить к выполнению участка подпрограммы, состоящего из операторов VI_б30 VI_a31 VI_б32 VI_a33 (табл. 11, строка 7, рис. 327,6).

Схемы счета для решения частных вариантов задачи, сведенные в табл. 11, могут быть объединены в одну схему счета, представляющую обобщенный алгоритм:

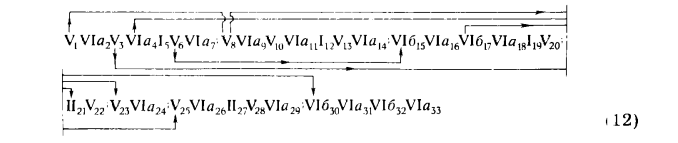
Для наглядности и выявления структуры построения обобщенного алгоритма для решения задачи по определению точки встречи прямой с плоскостью полученную схему счета целесообразно представить графически в виде "дерева", устанавливающего связь между исходными данными задачи и алгоритмом ее решения (рис. 328).

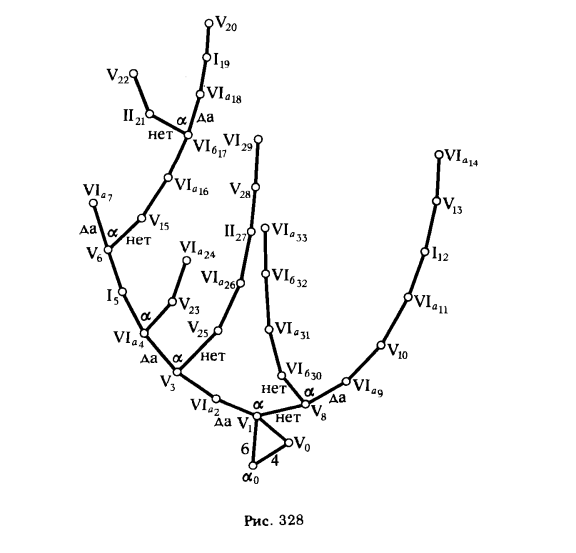
Из приведенной схемы видно, что машина сможет самостоятельно выбрать правильный путь решения, если программа будет составлена так, чтобы она начала работать по "жесткой" подпрограмме (5) основного (вариант I) алгоритма. После выполнения оператора V₁ выполняется проба α, позволяющая выяснить, определяется ли точка в результате его выполнения*. Если да, то машина приступает к выполнению оператора VI_a2, если нет, то ей следует выполнять оператор V₈. Аналогичные пробы выполняются и после операторов V₃, VI_a4 , V₆. По результатам этих проб машина либо продолжает решение по основной програм-ме, если точка определена, либо приступает к выполнению другого участка программы, когда точка не получена. Выбор нового участка зависит от того, при выполнении какого оператора не получена новая точка пересечения.

Пользуясь схемой счета (12) обобщенного алгоритма, машина самостоятельно решает любую задачу по нахождению точки встречи прямой с плоскостью, независимо от характера расположения исходных данных и варианта задания плоскости **.

Нахождение точки встречи прямой с плоскостью является элементарной, но часто встречающейся задачей, входящей в состав алгоритма для решения более сложных задач, например, задач по определению линии сечения линейчатой поверхности плоскостью.

Обозначим через R схему счета (алгоритм) для решения задачи по нахождению точки встречи прямой с плоскостью. Тогда в общем случае алгоритм для решения задачи по определению линии сечения линейчатой поверхности плоскостью в символической форме может быть записан:

∑₀(α_i); ∑₁(P_i); ∑₂(S_i); ∑₃(RP_i); (13)

где ∑₀(α_i); — различные пробы, позволяющие выбрать правильный путь решения в зависимости от вида и характера расположения исходных данных; ∑₁(P_i); — логическая последовательность элементарных операций для нахождения точки, через которую проходит прямолинейная образующая линейчатой поверхности; ∑₂(S_i); — последовательность выполнения операторов I или II для нахождения проекций прямолинейных образующих;∑₃(RP_i); — вспомогательные операции.

Выполнение R для всех задач рассматриваемого типа одинаково, оно может меняться только в пределах вариантов задания и расположения секущей плоскости. При определении сечения линейчатой поверхности плоскостью задача сводится к многократному выполнению подпрограммы R — определению точки встречи прямой с плоскостью. Содержание (∑₁, ∑₂, ∑₃ ) продиктовано задачей определения частных положений последовательности прямолинейных образующих линейчатой поверхности; очевидно, для различных поверхностей оно будет различным.

Проследим изменение ∑₁, ∑₂, ∑₃ в зависимости от вида линейчатой поверхности.

* На схеме (рис. 328) указаны также проба α₀ и оператор V₀, α₀ — проба на число геометрических образов, заданных на чертеже. Если N = 4, то прежде чем приступить к выполнению основной программы, необходимо определить координаты точки схода следов (оператор V₀).

** Исключение составляют два случая: если плоскость, проходящая через ось х, задана следами; если пересекающая плоскость прямая — профильная.

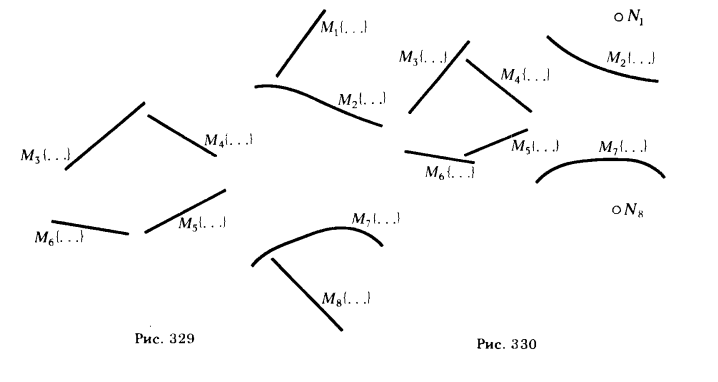
ПРИМЕР 1. Определить сечение цилиндрической поверхности плоскостью (рис. 329).

Для определения линии сечения произвольной цилиндрической поверхности плоскостью может быть рекомендован следующий план машинного решения задачи:

1) из массива ячеек памяти, где хранятся координаты растрэлементов, принадлежащих горизонтальной проекции криволинейной направляющей (множества M₇ { ... } ), выбрать точку 1'₁, имеющую минимальное значение х;

2) найти на фронтальной проекции криволинейной направляющей M₂{...} точку 1'₁ с х= x_(.)l'₁;

3) определить уравнение прямой n ∋ 1'₁ и || прямой, определяемой множеством растрэлементов M₈{...} ;

4) определить уравнение прямой n"₁ ∋ 1"₁ и || прямой М₁{...} ;

5) найти точку встречи прямой n₁ с плоскостью α, заданной пересекающимися прямыми, представленными множествами М₃{...}, М₄{...} и М₅{...} , М₆{...}.

Чтобы найти вторую точку, принадлежащую искомой линии сечения, нужно определить уравнения проекции следующей прямолинейной образующей поверхности. Для этого повторяем операции, предусмотренные пп. 1...4. Для определения положения второй (n'₂) и всех последующих (n'₃, n'₄, .... n'_n) проекций прямых берем на кривой М₇{...} следующую из записанных точку (растрэлемент). После того, как будут определены уравнения проекций n'₂ и n"₂ (n'₂ || n'₁ и n"₂ || n"₁), машина приступает к выполнению п. 5. Цикл из операций, предусмотренных в пп. 1... 5, выполняется до тех

пор, пока на кривой M₇{...} не останется ни одной точки. Тогда в символике машинных операторов операции ∑₁, ∑₂, ∑₃ можно записать:

∑₁(P_i) - П III X I V; * (14)

∑₂(S_i) - II II; (15)

∑₃(RP_i) - R. (16)

Схема счета программы для решения поставленной задачи примет вид

П₁ III₁ X₃ I₄ V₅ II₇ R₈ (17)

Цикл П ... R₈ выполняется до тех пор, пока в М₇ {...} не останется ни одной точки.

ПРИМЕР 2. Определить сечение конической поверхности плоскостью (рис. 330) Отличие решения этой задачи от предыдущей будет состоять лишь в том, что выражение (15) может быть записано ∑₂(S_i) — II и схема счета примет вид

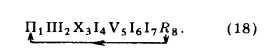
ПРИМЕР 3. Определить сечение однополостного гиперболоида плоскостью (рис. 331).

Для определения характера и последовательности выполнения операторов, входящих в ∑₁, ∑₂ и ∑₃ воспользуемся свойством направляющих рассматриваемой поверхности, состоящим в том, что если спроецировать точку, взятую на одной из трех направляющих (принад-

* П — операция обращения к первой записанной в М₇{...} массиве точке.

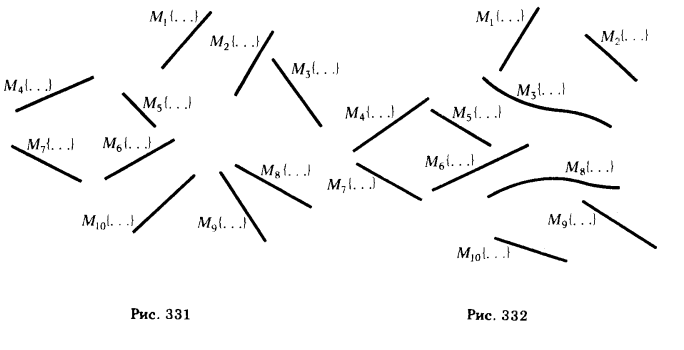
лежащих одному семейству), на плоскость α в направлении двух других направляющих и полученные точки соединить с соответствующими проекциями (следами) двух других направляющих, то полученные прямые будут принадлежать второму семейству образующих.

Точки пересечения соответственных прямых, принадлежащих разным семействам, определяют кривую второго порядка — сечение однополосного гиперболоида плоскостью а. В этом случае выражения (14), (15) и (16) примут вид

∑₁(P_i) - П III V I V;

∑₂(S_i) - П II II II;

∑₃(RP_i) - R R R R I I V III V.

для превого цикла, а для всех последующих циклов.

∑₃(RP_i) - R R I I V III V.

Схема счета программы запишется в виде

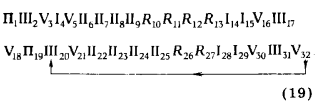
ПРИМЕР 4. Определить сечение коноида плоскостью (рис. 332).

Решение этой задачи аналогично предыдущей с той лишь разницей, что точки следует брать на криволинейной направляющей и проецировать их на секущую плоскость в направлении прямолинейной направляющей коноида.

Схема счета в этом случае примет вид

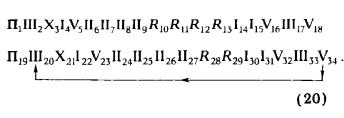
Чтобы машина самостоятельно (без участия человека) могла выбрать правильный путь решения задачи, ей должна быть известна поверхность, линию пересечения с которой требуется определить. Признаками, с помощью которых машина сможет "распознать" по эпюру Монжа, с какой поверхностью она имеет дело при решении задачи, служат:

1) присутствие точечного образа;

2) отсутствие криволинейных образов;

3) число криволинейных образов.

Эти признаки положены в основу проб, составляющих содержание ∑₀(α_i) [из выражения (13)], которые должна выполнить машина для выбора нужного варианта решения.

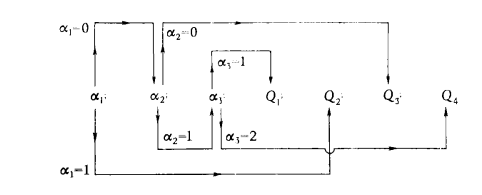
Обозначим:

а) схемы счета (17) — Q₁; (18) — Q₂; (19) — Q₃; (20)— Q₄ ;

б) пробы: α₁ — проба на наличие точечного образа, если точечный образ есть (α₁ = 1), то выполняется массив Q₂, если нет (α₁ = 0), то следует переходить к пробе α₂; α₂ — проба на наличие криволинейного образа, если такой образ есть (α₂ = 1), то необходимо выполнять пробу α₃, если нет (α₂ = 0), то машина должна приступить к выполнению массива Q₃; α₃ — проба на число криволинейных образов, если образ один (α₃ = 1), то выполняется массив Q₁,если два (α₃ = 2), то машина приступает к выполнению массива Q₄.

Вариант задания секущей плоскости не влияет на характер поиска, так как при составлении признаков прямолинейные образы не учитывались. В общем виде схема счета программы для решения рассмотренных задач примет вид