Примеры построений в изометрической и диметрической проекциях

Ниже приведены некоторые примеры построений в прямоугольных изометрической и диметрической проекциях.

I. Проекция сферы. На рис. 473 сверху дано изображение сферы в изометрической и диметрической проекциях.

В обоих случаях сфера показана с вырезом одной восьмой части. Окружности, представляющие собой очерк проекции, проведены: для изометрической проекции радиусом, равным

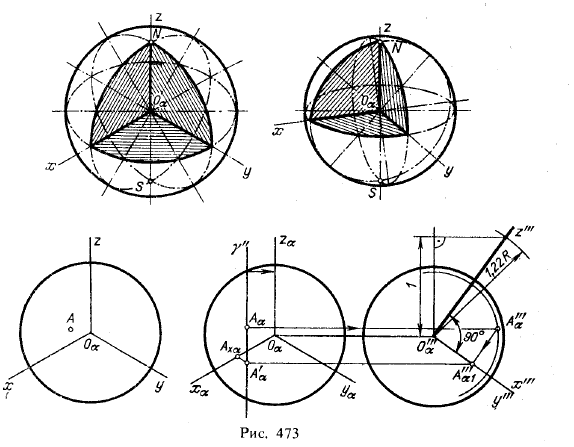
1,22R, для диметрической проекции радиусом 1,06R, где R — радиус сферы. Эллипсы в обоих случаях соответствуют экваториальному и двум меридиональным сечениям.

На рис, 473 внизу слева дано изображение сферы в изометрической проекции; на видимой стороне сферы дана точка А. Справа показано построение вторичной проекции А'_α (см, рис, 449) и трехзвенной координатной ломаной линии А_αА'_αА_хαО_α, что дает возможность определить прямоугольные координаты точки А в пространстве. Построение выполнено в предположении, что плоскость изометрических проекций занимает фронтальное положение и что равнонаклоненнью к ней оси х, у, z прямоугольных координат спроецированы не только на эту плоскость, но и на дополнительную профильную плоскость π₃. Получается система плоскостей проекций α, π₃ и проекции А_α и А'"_α заданной точки А, причем А'"_α получена при помощи сечения сферы пл. γ. Вторичная проекция точки А также изображена двумя проекциями: А'"_α1 и А'_α

2. Линии пересечения цилиндра и конуса плоскостью. На рис, 474 и 475 показано построение в изометрической проекции линий пересечения цилиндра и конуса фронтально-проецирующими плоскостями ¹). В рассматриваемых случаях линии пересечения представляют собой эллипсы.

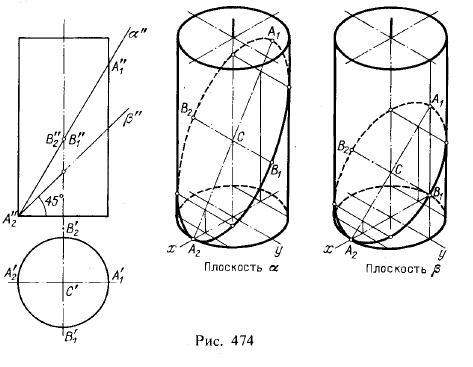
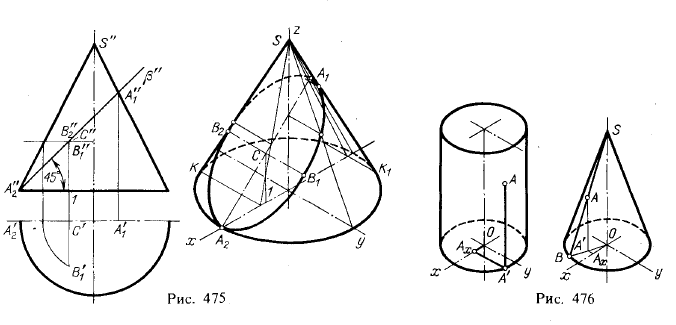
Прежде всего, руководствуясь чертежом, наносим по координатам точек А₁ и А₂ линии наклона ллоскостей α и β. Для построения точек эллипсов берем вспомогательные секущие плоскости: для цилиндра — параллельно его образующим и плоскости yOz, для конуса — про-

¹) Построение выполнено в приведенных коэффициентах искажения.

ходящие через его вершину параллельно оси у. Эти плоскости задаются их следами, параллельными оси у, на плоскостях оснований цилиндра и конуса.

При таком выборе вспомогательных плоскостей прямые, по которым они пересекаются с плоскостями α и β, получаются параллельными оси γ. В пересечении этих прямых с образующими цилиндра и конуса получаются точки эллипса.

В первую очередь следует найти такие характерные точки, как отмеченные на чертежах буквами А₁, А₂. В₁ и В₂, а также получаемые на очерковых линиях изометрической проекции. Малая полуось получаемого в сечении эллипса, равная С'В'₁, сохраняет свою величину и в изометрической проекции (С'В'₁ = СВ₁). Но свое значение малой оси для эллипса в изометрической проекции отрезок В₁В₂ сохраняет лишь при пл. β, т. е. при указанном на рисунке угле наклона этой плоскости, равном 45°.

Действительно, в этом случае отрезок В₁В₂ будучи параллельным оси у, остается и в изометрической проекции перпендикулярным к A₁A₂, следовательно, отрезки A₁A₂ и В₁В₂ сохраняют свое значение осей эллипса. В случае же иного наклона плоскости, как это показано на цилиндре для пл. α, отрезки А₁А₂ и В₁В₂ в изометрической проекции не являются осями эллипса, а лишь его сопряженными диаметрами.

3. Построение координатных отрезков для точки, заданной на поверхности цилиндра и конуса вращения в аксонометрической проекции. На рис. 476 даны примеры для цилиндра и конуса в изометрической проекции. Во всех случаях начало координат взято в центре основания (точка О).

Через заданную на цилиндре точку А проведена прямая параллельно оси z, и из вторичной проекции А' проведена прямая шраллельно оси γ до пересечения с осью х. Отрезки 0А_x, А_xА' и А'А позволяют определить координаты точки А в данной системе осей координат.

Через заданную на конусе точку А проведена образующая и построена вторичная проекция (ОВ) этой образующей. Проводя из точки А перпендикуляр до пересечения с ОВ, получаем вторичную проекцию точки А. Дальнейшее ясно из чертежа.

На рис. 477 показано построение координатных отрезков для точки, заданной на поверхности усеченного конуса вращения в изометрической проекции (рис. 411, а). Положим, что мы имеем сечение конуса плоскостью, проходящей через ось

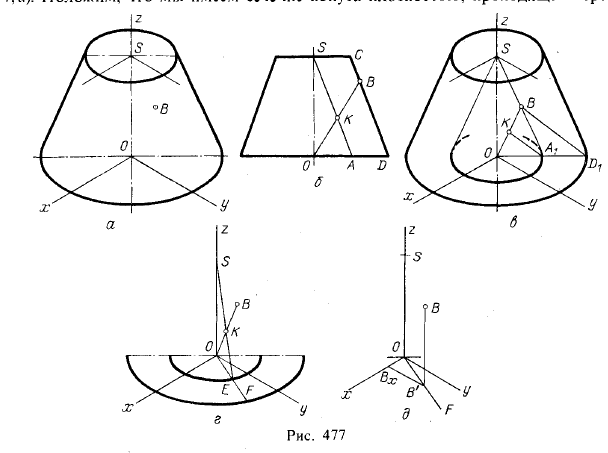
конуса и точку В (рис. 477,6). В полученной трапеции проведена прямая SA || CD и пересекающая ее в точке К прямая ОВ. Получаем OK : KB = OA : AD. Но эта пропорция сохранится в изометрической проекции. Построим конус с вершиной в точке S и с образующей, параллельной образующей усеченного конуса (рис. 477, в). От

ношение OA₁: A₁D₁ повторяет отношение OA : AD, содержащееся в указанной выше пропорции. Теперь можно получить точку К на ОВ на рис. 477, в. Образующая, проведенная через точки S и Е, определяет точку К (рис. 477, г) и проекцию OF образующей, на которой находится точка В. Отсюда мы получаем возможность получить вторичную проекцию В' (рис. 477, д) и координатные отрезки ВВ', В'В_x и ОВ_х, определяющие координаты z, у и х.

Указанное построение дается на случай, если нельзя достроить усеченный конус до полного. Если достроить можно, то построение производится, как показано для конуса на рис. 477,6.

4. Примеры построения линий пересечения цилиндрических и конических поверхностей вращения между собой. Линии пересечения строят по точкам; эти точки находят или по их координатам, взятым с ортогональных проекций, или способом вспомогательных секущих плоскостей непосредственно в аксонометрических проекциях. Последнее показано на рис. 478, а — г.

Вспомогательные секущие плоскости пересекают данные цилиндры и конусы по образующим линиям. На рис; 478, а оси цилиндров пересекаются, на рис. б) скрещиваются. Если на рис. а) точки А и А₁ определялись при помощи секущей плоскости, проходящей через оси обоих цилиндров, то на рис. б) надо учесть смещение на

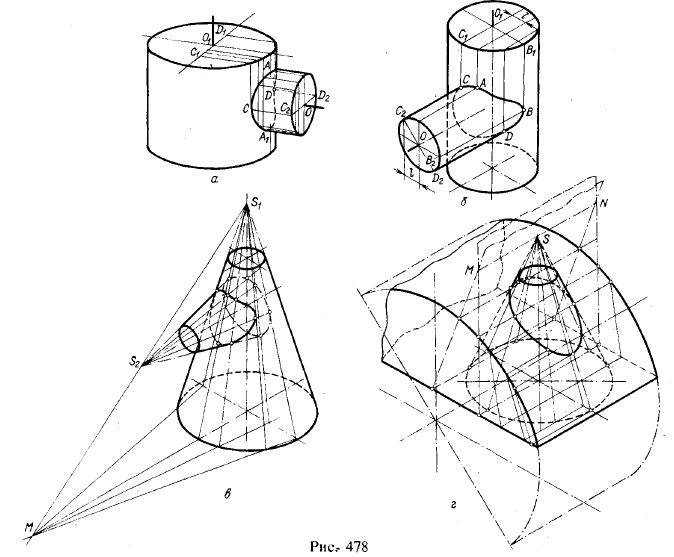
l ¹). На рис. 478,в секущие плоскости проходят через прямую S₁S₂, а их следы на плоскости основания конуса с вершиной S₁ проходят через след прямой S₁S₂ на этой плоскости. На рис. 478, г плоскости проходят через прямую MN, проведенную через вершину конуса — точку S — параллельно образующей цилиндра.

¹) Разметка точек буквами произведена лишь для пояснении.

5. Построение точек касания окружности — очерка проекции сферы — с эллипсом — проекцией окружности, получаемой на сфере при пересечении ее плоскостью. На рис. 479, а показана сфера, срезанная тремя плоскостями - профильной (γ), горизонтальной (δ) и фронтально-проецирующей (β). По этому чертежу построена: изометрическая проекция (рис. 479,6) в приведенных коэффициентах искажения. Эллипс m построен так, как было показано на рис. 469, а эллипс n — как на рис. 465. Проекция сферы дана очерком — окружностью радиуса равного 1,22R. Эта окружность касается эллипса m в точке К, эллипса n — в точке L.

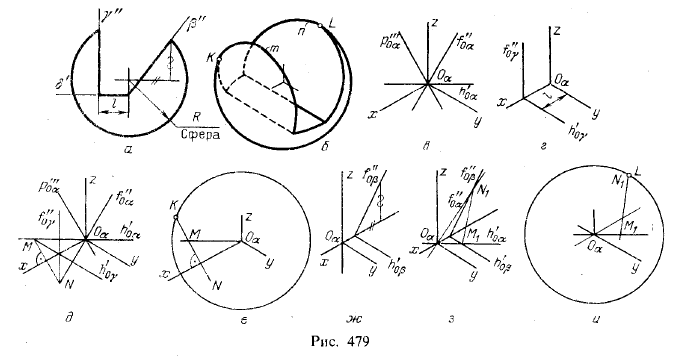
Рассмотрим, как найдена точка К. Она получена на окружности — очерке проекции сферы, т. е. в плоскости изометрической проекции (α), и в то же время на эллипсе m т. е. в пл. γ, пересекающей сферу. Но если точка принадлежит одновременно двум плоскостям, то она принадлежит линии пересечения этих плоскостей.

Плоскость изометрической проекции, как известно, равнонаклонна к π₁, π₂ и π₃. Треугольник следов этой плоскости равносторонний (см. рис. 457). Отнеся пл. α к точке О_α, т. е. к началу осей и центру сферы, помучим положение следов, указанное на рис. 479, в.

Пл. γ в системе тех же осей изобразится в следах, как показано на рис. 479,г. Совместим рис. в) и г) и построим линию пересечения плоскостей α и γ (рис. 479, е): прямая MN проходит через точку M пересечения горизонтальных следов параллельно следу р"'_0α, так как γ||π₃ (при этом р"'_0α⊥O_αX. следовательно, MN⊥О_αх).

Теперь остается найти точку К в пересечении прямой MN с окружностью — изометрической проекцией сферы (рис. 479, е).

Для определения положения точки L (см. рис. 479, б) надо изобразить в системе изометрических осей фронтально-проецирующую пл. β (рис. 479,.ж), а затем найти прямую пересечения плоскостей α и β (рис. 479, з), эта прямая проходит через точку M₁ пересечения следов h'_0β и h'_0α и через точку N₁ пересечения следов f"_0β и f"_0α. Искомая точка L получается в пересечении прямой M₁N₁ с окружностью — изометрической проекцией сферы (рис. 479, и).