Пересечение конической поверхности плоскостью. Построение развертки

Для построения кривой линии, получаемой при пересечении конической поверхности плоскостью, следует в общем случае находить точки пересечения образующих с секущей плоскостью.

Если плоскость, пересекающая коническую поверхность, проходит через вершину этой поверхности, то получаются две прямые — образующие (рис. 368, АА₁ и ВВ₁)

Рассмотрим пример построения, которым иллюстрируется такое пересечение конической поверхности.

Положим, что в плоскости, заданной точкой S и горизонтальной прямой MN (рис. 368, справа), надо провести через точку S прямую, составляющую с пл. π₁ некоторый угол φ.

Геометрическим местом прямых, составляющих угол φ с пл. π₁, является коническая поверхность вращения, ось которой перпендикулярна к пл. π₁ и вершиной, до условию, должна быть точка S. Следовательно, заданная плоскость проходит через вершину конуса и рассекает его поверхность по прямым — образующим. Эти прямые и будут искомыми: они проходят через точку S в заданной плоскости под заданным углом φ к пл. π₁

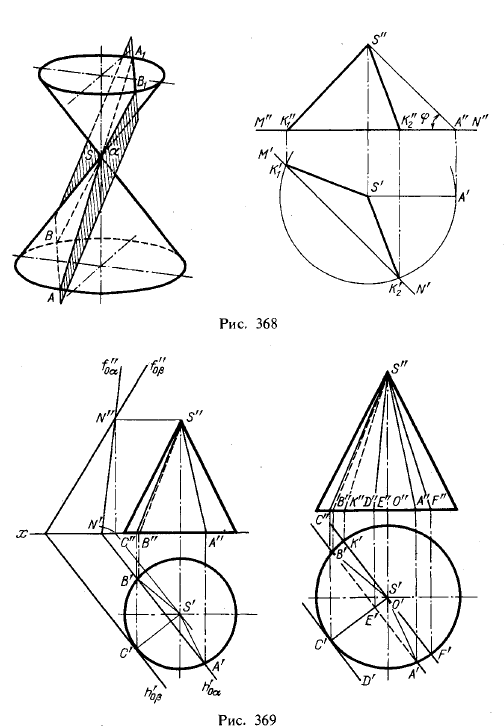
Теперь остается изобразить конус (он изображен частично), для чего проведена прямая S" А" и дуга окружности из точки S', как из центра, радиусом S'A', причем основание конуса взято в горизонтальной плоскости, проходящей через заданную прямую MN.

Остальное ясно из чертежа. Данное построение сравните с выполненным на рис. 245 и 246 в § 38.

На рис. 369 слева изображен прямой круговой конус, поставленный на пл: π₁. Пл. β является касательной к данному конусу; касание происходит по образующей SC, след h'_0β касается окружности — горизонтальной проекции основания конуса; то, что точка S лежит в пл. β, устанавливается при помощи горизонтали SN. Пл. а проходит через вершину данного конуса и пересекает его по образующим SA и SB.

На том же рисунке справа плоскости показаны не в следах. Плоскость, касательная к конусу, задана образующей SC и прямой CD, касательной к окружности основания конуса. Плоскость, проходящая через вершину и рассекающая конус по образующим SA и SB, задана прямой АВ в плоскости основания конуса и прямой SE, проходящей через вершину конуса и пересекающей прямую АВ в точке Е.

Если плоскость проходит через ось конуса, то она его пересекает по образующим с максимальным для данного конуса углом между ними. На рис. 369 справа это — образующие SF и SK; угол между ними равен углу с вершиной между очерковыми прямыми в фронтальной проекции конуса.

Если же конус вращения пересекается плоскостью, не проходящей, через его вершину, то в пересечении получается одна из следующих четырех кривых: 1) эллипс, если секущая плоскость пересекает все образующие одной полости поверхности или, иначе, не параллельна ни одной из образующих конуса (рис. 370, плоскости α,α₁ и α₂); в этом случае угол между секущей плоскостью и осью конуса больше угла между этой осью и образующей конуса; 2) окружность¹), если секущая плоскость перпендикулярна к оси конуса (рис. 370, плоскость α₃); 3) парабола, если секущая плоскость параллельна только одной из образующих (рис. 370, пл. γ); в этом

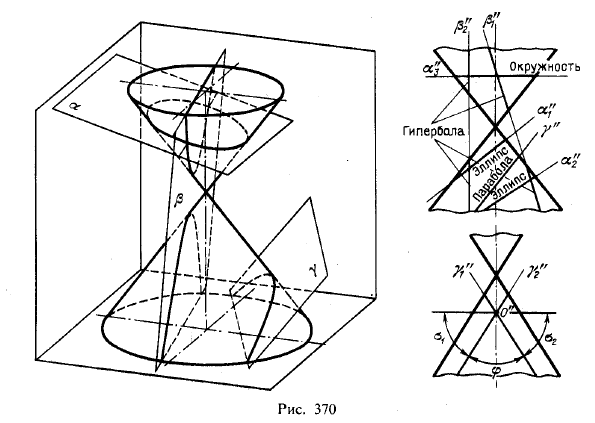
случае углы между секущей плоскостью и осью конуса и между этой осью и образующей конуса равны между собой; 4) гипербола, если секущая плоскость параллельна двум образующим (рис. 370, плоскости β, β₁ и β₂); при этом угол между секущей плоскостью и осью конуса меньше угла между этой осью и образующей конуса.

На рис. 370 справа внизу показаны углы φ, σ₁ и σ₂. Угол φ — между следами γ"₁ и γ"₂ плоскостей, пересекающих конус по параболам. Если проводить следы через точку О" внутри угла φ, то этим определяются плоскости, пересекающие конус по гиперболам, а если через точку О" внутри углов σ₁ и σ₂, то по эллипсам.

Рассмотрим доказательство того, что при пересечении конуса вращения плоскостью, не параллельной ни одной из его образующих (и не проходящей через его вершину), получается эллипс.

Как бы в данном случае ни были расположены в пространстве конус и секущая плоскость, всегда можно преобразованием чертежа привести их в положение, когда ось конуса окажется перпендикулярной к пл. π₁, а секущая плоскость — фронтально-проецирующей. Именно в таком положении показаны конус и пересекающая его пл. γ на рис. 371, причем даны две проекции конуса — фронтальная и профильная.

') Можно рассматривать как эллипс с равными в пределе осями.

В конус вписаны сферы, касательные к пл. γ в точках F₁ и F₂, а к конусу — по параллелям, проходящим соответственно через точки К₁ и К₂. Точки F₁ и F₂ получаются в плоскости главного меридиана и, следовательно, расположены на одной прямой с точками А₁ и A₂, принадлежащими фигуре сечения конуса пл. γ. Эта фигура сечения проецируется на пл. π₂ в виде отрезка А"₁А"₂.

Рассмотрим образующую конуса, лежащую в профильной плоскости, и отметим на ней точки К₁ и К₂, в которых вписанные шары касаются этой образующей, и точку М, принадлежащую той же образующей и кривой сечения конуса пл. γ. Известно, что отрезки касательных, проведенных из какой-либо точки к сфере, определяемые этой точкой и точками касания, равны между собой. Отсюда MK₁ = MF_l и MK₂ = MF₂. Складывая почленно, получаем MK₁ + МК₂ = MF₁ + MF₂. Но МК₁ + МК₂ = K₁K₂, т. е. сумма расстояний некоторой точки, взятой на кривой сечения, до двух постоянных точек F₁ и F₂, принадлежащих плоскости этого сечения, является величиной постоянной, равной в данном случае отрезку К₁К₂.

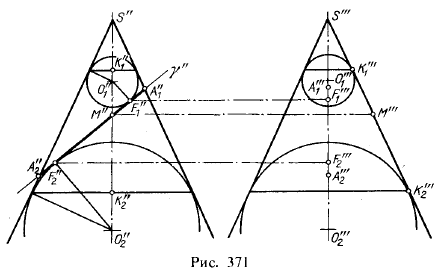
Этот отрезок образующей конуса расположен между двумя его параллелями и не зависит от выбора точки М на кривой сечения. Действительно, если на кривой сечения конуса была бы взята не точка М, а другая точка, то проходящая через нее образующая кйснулась бы обеих сфер в точках на тех же параллелях. Отрезок этой образующей между точками касания был бы равен тому же отрезку К₁К₂

Сделанный вывод показывает, что точка М принадлежит геометрическому месту точек, сумма расстояний которых до двух данных точек имеет некоторое постоянное значение. Это соответствует определению эллипса.

Подобным образом делаются выводы и для случаев пересечения конуса вращения по параболе и гиперболе.

На рис. 372 изображен конус вращения с сечением его фронтально-проецирующей плоскостью. Точки пересечения следа β" с фронтальными проекциями образующих представляют собой проекции точек искомой кривой пересечения, в данном случае эллипса. По этим проекциям найдены проекции на плоскостях π₁ и π₃.

Одна из осей эллипса (большая) проецируется на пл. π₂ отрезком К"Р". Другая (малая) ось эллипса, перпендикулярная к пл. π₂, проецируется в одну точку — в середину отрезка К"Р".

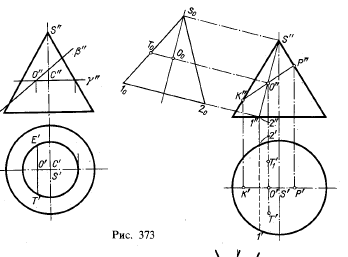
Если провести пл. γ через точку О перпендикулярно к оси конуса (в данном случае параллельно пл. π₁ то проекция малой оси получится (рис. 373) как хорда Т'Е' окружности — горизонтальной проекции сечения конуса пл. γ.

Проекцию малой оси можно получить также построением, показанным на рис. 373 справа. Конус пересечен по треугольнику, повернутому и наложенному на пл. π₂. Отрезок О₀Т₀ равен малой полуоси. Откладывая этот отрезок от точки О' перпендикулярно к К'Р', получаем малую ось (Т'Т'₁ = 2О₀Т₀).

Проекции фигуры сечения на пл. 7π₁ и π₃ — эллипсы. Проекция на π₃ может оказаться и окружностью: в этой проекции при некотором наклоне секущей плоскости проекции осей эллипса могут оказаться равными. Проекция же фигуры сечения

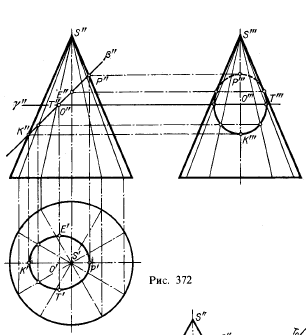
(эллипса) на плоскости, перпендикулярной к оси конуса (в данном случае на пл. π₁), окружностью быть не может ¹).

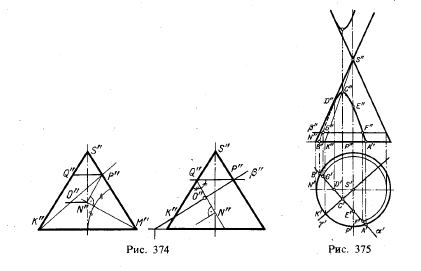
На рис. 374 слева показано, как для некоторого конуса найти направление фронтального следа фронтально-проецирующих плоскостей, пересекающих этот конус по эллипсам, проецирующимся на π₃ в виде окружности. Построение производится на фронтальной проекции конуса. Биссектриса угла S"M"K" пересекает ось симметрии проекции в точке N". Проведя в этой точке перпендикуляр к биссектрисе M"N", находим точку Р". Прямая, проведенная через точки К" и Р", дает направление для фронтальных следов искомых секущих плоскостей. Дело сводится к построению диагонали равнобочной трапеции К"M"P"Q", в которую можно вписать окружность с центром в точке N". Проводя через точку N" прямую параллельно Q"P", получим точку О" — проекцию центра эллипса, фронтальная проекция которого — отрезок К"Р".

Будет ли проецироваться на π₃ в виде окружности эллипс, получаемый при пересечении конуса пл. β (рис. 374, справа)? Построение на рис. 374 дает один из приемов проверки: через точку Р" проводим прямую, параллельную основанию, проводим биссектрису угла P"Q"K", получаем точку N". Так как перпендикуляр, проведенный в точке N" к этой биссектрисе, не проходит через точку К", то проекция сечения на π₃ окажется эллипсом, а не окружностью.

На рис. 375 показано построение фронтальной проекции гиперболы, полученной при пересечении конуса вращения горизонтально-проецирующей плоскостью.

Так как горизонтальная проекция гиперболы совпадает со следом α', то в пересечении α' с горизонтальной проекцией основания определяются точки А' и В', а по ним проекции А" и В":

Для нахождения точки С" — наивысшей точки проекции гиперболы на пл. π₂ — проведена вспомогательная горизонтально-проецирующая пл. γ через ось конуса перпендикулярно к следу α'. Горизонтальная проекция С' искомой точки С получается в пересечении α' и γ'; найдя фронтальную проекцию образующей SK, отмечаем на ней точку С".

Далее, определена точка D", в которой фронтальная проекция гиперболы разделяется на видимую и невидимую части. Эта точка находится при помощи образующей SN.

Для нахождения других точек гиперболы можно провести несколько образующих в пределах той части поверхности конуса, которая отмечена буквами SAKB, или несколько вспомогательных секущих плоскостей. На рис. 375 указана одна из таких вспомогательных плоскостей — горизонтальная пл. β, пересекающая поверхность конуса по окружности. При помощи этой плоскости найдены точки F и G.

На второй полости конической поверхности получается вторая ветвь гиперболы.

На рис. 376 показано построение проекций фигуры сечения прямого кругового конуса плоскостью общего положения, заданной горизонталью АС и фронталью АВ, и натурального вида фигуры сечения.

Построение выполнено при помощи способа перемены плоскостей проекций. Введена дополнительная плоскость проекций π₃, выбранная так, чтобы она была перпендикулярна не только к пл. π₁ но и к секущей плоскости: ось π₃/π₁ проведена перпендикулярно к проекции А'С. На пл. π₃ секущая плоскость проецируется в виде прямой, на которой расположена проекция фигуры сечения (отрезок 1"'2"'). Этим определена болыцая ось эллипса, по которому конус пересекается данной плоскостью. В точке О'", делящей отрезок 1'"2'" пополам, находится проекция центра эллипса. Плоскость β, проведенная перпендикулярно к оси конуса, позволяет найти малую ось эллипса (на рис. 376 проведена полуокружность и в ней отрезок 0"'3"' равный половине малой оси эллипса). По точкам 0"\ Г", 2"' найдены проекции О', Г, 2', а затем проекции О"', 1"', 2"', отстоящие от оси п₂/п₁ на то же расстояние, на каком находятся проекции О'", 1"', 2"' от оси π₃/π₁. Точка 2" — наивысшая на фронтальной проекции, точка 1" — наинизшая из точек эллипса — фронтальной проекции

¹) Интересующихся доказательством отсылаем к предыдущим изданиям.

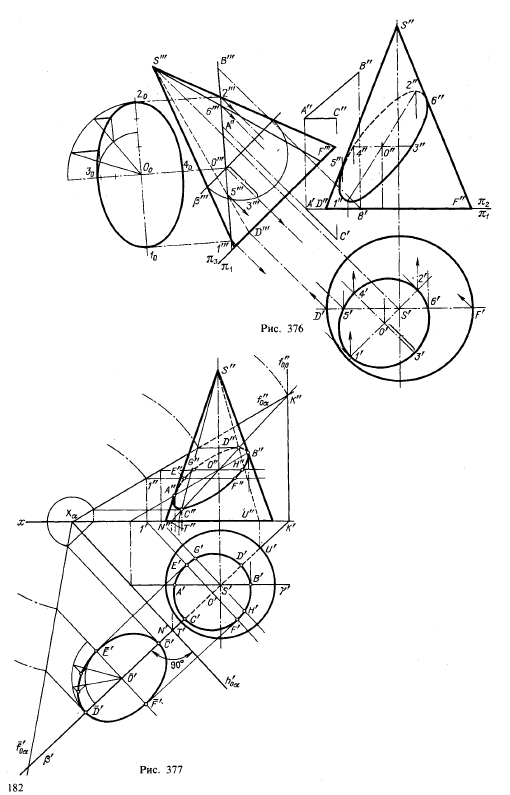
сечения. Для определения положения точек 5" и 6", в которых эллипс на фронтальной проекции разделяется на «видимую» и «невидимую» части, построены проекции S"'D"' и S"'F"' образующих SD и SF, найдены точки 5"' и 6"', по ним проекции 5' и 6' и затем 5" и 6". Но можно было найти хотя бы только точку 5" и провести через нее прямую, параллельную проекции А"В", так как плоскость главного меридиана конуса пересекает данную секущую плоскость по фронтали.

Малая ось эллипса проецируется на пл. π₁ в свою натуральную величину (отрезок 3'4'), располагаясь на горизонтальной секущей плоскости, и является также малой осью для эллипса — горизонтальной проекции фигуры сечения. Натуральный вид этой фигуры получен построением эллипса по его большой оси (1₀2₀ = 1"'2"') и малой оси (3₀4₀ = 3'4').

На рис. 377 показано аналогичное построение при задании секущей плоскости ее следами.

Построение проекций сечения начато с нахождения точек, лежащих на очерке фронтальной проекции конуса. Для этого проведена через ось конуса вспомогательная секущая плоскость γ, параллельная пл. π₂, след этой плоскости — γ'. Пл.γ пересекает пл. α по фронтали, а конус — по двум образующим. Точки А и В, получающиеся при пересечении фронтали с образующими, принадлежат искомой линии пересечения конуса с плоскостью α.

В точках А" и В" фронтальная проекция линии пересечения касается очерка фронтальной проекции конуса и разделяется на две части: видимую и невидимую. Далее, построены еще две характерные точки ¹), а именно высшая и низшая точки сечения, для чего проведена вспомогательная секущая пл. β, горизонтально-проецирующая, перпендикулярная к следу h'_0α и проходящая через ось конуса. Пл. β рассекает конус по образующим ST(S"T", S'T) и SU (S"U", S'U'), а пл. α — по линии NK(N"K", N'K'). Точки С и D, получающиеся в пересечении образующих ST и SU с прямой NK, будут искомыми точками. Отрезок CD является большой осью эллипса, получающегося при пересечении данного конуса пл. α. Проекция CD' является большой осью эллипса — горизонтальной проекции фигуры сечения. Разделив CD пополам, получим положение центра эллипса; точки О" и О' являются центрами эллипсов — проекций фигуры сечения.

Для нахождения промежуточных точек линии пересечения удобно пользоваться горизонтальными секущими плоскостями, так как они пересекают поверхность конуса по окружностям, а пл. α — по горизонталям. Пригодны для этого построения лишь те плоскости, у которых фронтальные следы помещаются в пределах между С" и D", так как в данном случае выше точки D" и ниже точки С" не может быть точек, принадлежащих линии пересечения. На рис. 377 показано построение точек Е, F, G, Н при помощи двух таких плоскостей; одна из них проведена через точку О, благодаря чему определен отрезок E'F', представляющий собой малую ось эллипса, получающегося при пересечении конуса ил. α, и в то же время малую ось горизонтальной проекции этого эллипса.

Отрезки C"D" и E"F" являются сопряженными диаметрами для эллипса — фронтальной проекции фигуры сечения. По ним можно найти оси эллипса ²).

Натуральный вид сечения найден совмещением секущей плоскости с пл. π₁. Эллипс может быть построен по большой и малой осям, длины которых найдены путем совмещения концевых точек осей C' и D' для большой оси, E' и F' — для малой.

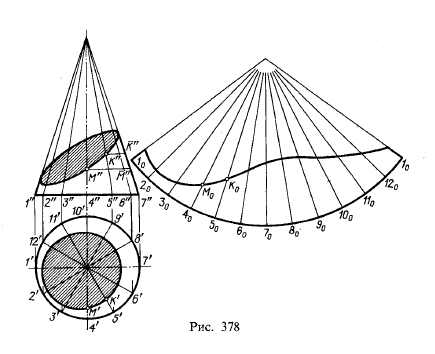
На рис. 378 показано построение развертки. Боковая поверхность развертывается в круговой сектор. Угол сектора подсчитывается по формуле 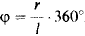,где r — радиус окружности основания конуса, а l — образующая конуса.

Для того чтобы нанести на развернутой боковой поверхности конуса линию сечения, проводят ряд образующих конуса и определяют длины их отрезков: затем наносят образующие на развернутую боковую поверхность конуса и откладывают длины отрезков этих образующих.

На рис. 378 построена развертка боковой поверхности и па ней нанесена линия сечения. Длина отрезков образующих определена поворотом образующих до положения, параллельного пл. π₂ (это построение показано для двух образующих).

¹) Характерными точками называют такие точки кривой пересечения, как наиболее удаленная и наиболее близкая к плоскости проекций, точки, делящие кривую на видимую и невидимую части, концы осей эллипсов.

²) О сопряженных диаметрах эллипса см. § 21.

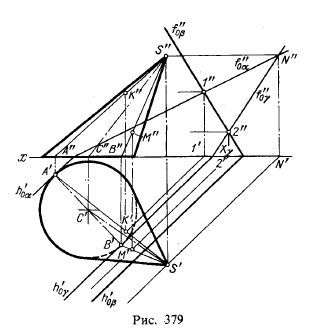
На рис. 379 показано нахождение наиболее и наименее удаленных от пл. π₁ точек кривой пересечения некоторого конуса плоскостью общего положения β. Для построения этих точек проведены касательные к конусу плоскостей α и γ так, что их следы h'_0α и h'_0γпараллельны h'_0β этим определяются те образующие конической поверхности, на которых должны находиться искомые точки К и М.

Сначала строятся горизонтальные проекции К' и М' в точках пересечения горизонтальных проекций горизонталей, по которым плоскости α и γ пересекают пл. β с горизонтальными проекциями образующих SA и SB, а затем на фронтальных проекциях этих образующих отмечаются проекции К" и М".

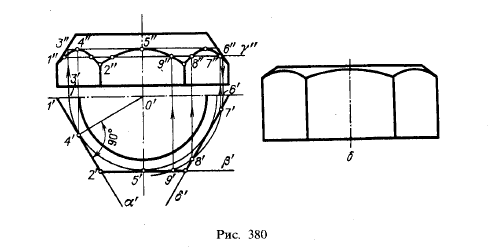
На рис. 380, а показано построение кривых, получающихся на поверхности конуса вращения при пересечении его гранями правильной шестиугольной призмы ¹). Две из боковых граней расположены в горизонтально-проецирующих плоскостях α и δ, а третья грань — во фронтальной пл. β. Положение этих плоскостей относительно оси конуса позволяет сразу определить, какие кривые получатся в пересечении. Получаются гиперболы, причем одна из них проецируется на пл. π₂ без искажения.

Для нахождения точек кривых взяты параллели на конусе. Прежде всего найдены крайние точки 1', 4', 2', 5' на горизонтальной проекции, а по ним определены точки 1", 4", 2", 5" на фронтальной проекции. Затем при помощи вспомогательной горизонтальной пл. γ определена сначала точка 6" на очерке фронтальной проекции конуса, затем получена точка 6' и при помощи окружности радиуса О'6' построены точки 7', 8' и 9', по которым найдены точки 7", 8" и 9".

На рис. 380,б изображена шестигранная гайка (дан только вид спереди); кривые, отделяющие боковые грани гайки от ее конической части, представляют собой гиперболы, построение проекций которых аналогично показанному на рис. 380, а.

Вопросы к § 57

1. В чем заключается общий прием построения кривой линии, получающейся при пересечении конической поверхности плоскостью?
2. Как надо провести плоскость, чтобы пересечь коническую поверхность по прямым линиям?
3. Какие кривые получаются при пересечении конуса вращения плоскостями?
4. В любую ли коническую поверхность можно вписать сферы?
5. Как строится малая ось эллипса, получаемого при пересечении конуса вращения плоскостью?
6. В какую кривую проецируется эллипс, получаемый при пересечении конуса вращения, на плоскость, перпендикулярную к оси конуса?
7. Как строится развертка боковой поверхности конуса вращения?
8. Что представляют собой кривые на гайке с конической фаской на ней?