Пересечение цилиндрической поверхности плоскостью. Построение развертки
ТеорияДля построения кривой линии, получаемой при пересечении цилиндрической поверхности плоскостью, следует в общем случае находить точки пересечения образующих с секущей плоскостью, как было сказано на с. 170 в отношении линейчатых поверхностей вообще. Но это не исключает возможности применять и вспомогательные плоскости, пересекающие каждый раз поверхность и плоскость.
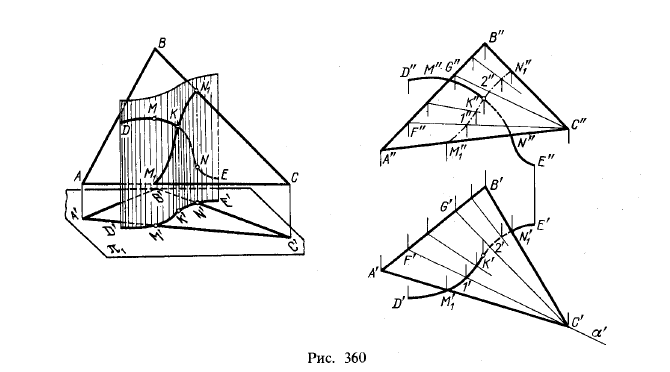
Прежде всего отметим, что любая цилиндрическая поверхность пересекается плоскостью, расположенной параллельно образующей этой поверхности, по прямым линиям (образующим). На рис. 360 показано пересечение цилиндрической поверхности плоскостью. В данном случае эта поверхность является вспомогательным элементом при построении точки пересечения кривой линии с плоскостью: через заданную кривую (см. рис. 360, слева) DMNE проведена цилиндрическая поверхность, проецирующая кривую на пл. π1. Далее, плоскость (на рис. 360 — треугольник) пересекает цилиндрическую поверхность по плоской кривой М1 ... N1. Искомая точка пересечения кривой с плоскостью — точка К — получается в пересечении кривых — заданной и построенной.
Такая схема решения задачи на пересечение кривой линии с плоскостью совпадает со схемой решения задач на пересечение прямой линии с плоскостью (см. §§ 23
и 25); в обоих случаях через линию проводят вспомогательную поверхность, которая для прямой линии является плоскостью.
Горизонтальная проекция кривой M1...N1, по которой цилиндрическая поверхность пересекается с плоскостью, совпадает с горизонтальной проекцией кривой D ... Е, так как эта кривая является направляющей для цилиндрической поверхности при перпендикулярных к пл. π1, ее образующих. Поэтому по точке М'1 на проекции А'С' мы можем найти проекцию М"1 на А"С" и по точке N'1 — проекцию N"1. Далее, на рис. 360 справа показана вспомогательная пл. α, пересекающая ABC по прямой CF, а цилиндрическую поверхность — по ее образующей с горизонтальной проекцией в точке 1'. В пересечении этой образующей с прямой CF получается точка с проекциями 1' и 1", принадлежащая кривой М1 ... N1 Очевидно, можно не указывать следа плоскости, а просто провести прямую в треугольнике, как это показано в отношении прямой CG, на которой получена точка с проекциями 2' и 2".
В рассмотренных далее примерах будут показаны развертки. Развертывание цилиндрической поверхности в общем случае может производиться по схеме развертывания поверхности призмы. Цилиндрическая поверхность как бы заменяется вписанной в нее или описанной призматической, ребра которой соответствуют образующим цилиндрической поверхности. Само развертывание, подобно показанному на рис. 283, производится при помощи нормального сечения. Но вместо ломаной линии проводится плавная кривая.
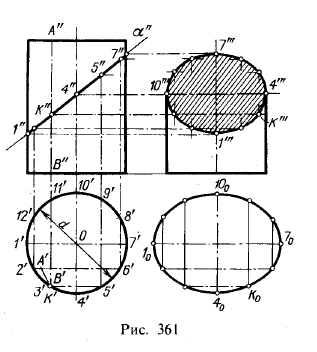
На рис. 361 показано пересечение прямого кругового цилиндра фронтально-проецирующей плоскостью. Фигура сечения представляет собой эллипс, малая ось которого равна диаметру основания цилиндра; величина большой оси зависит от угла между секущей плоскостью и осью цилиндра.
Так как ось цилиндра перпендикулярна к пл. π1 то горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией цилиндра.
Обычно для построения точек контура сечения проводят равномерно расположенные образующие, т. е. такие, проекции которых на пл. π1 являются точками, равноотстоящими друг от друга. Этой «разметкой» удобно пользоваться не только для построения проекций сечения, но и развертки боковой поверхности цилиндра, как это будет показано ниже.
Проекция фигуры сечения на пл. π3 — эллипс, большая ось которого в данном случае равна диаметру цилиндра, а малая представляет собой проекцию отрезка 1"7". На рис. 361 на пл. π3 изображение построено так, как будто верхняя часть цилиндра снята после пересечения его плоскостью.
Если бы на рис. 361 плоскость α составляла с осью цилиндра угол 45°, то проекцией эллипса на π3 была бы окружность. При этом отрезки 1"'7"' и 4"'10"' оказались бы равными.
Если тот же цилиндр пересекать плоскостью общего положения, также составляющей с осью цилиндра угол 45°, то проекцию фигуры сечения (эллипса) в виде окружности можно получить на дополнительной плоскости проекций, параллельной оси цилиндра и горизонталям секущей плоскости.
Очевидно, при увеличении угла наклона секущей плоскости к оси отрезок 1"'7"' уменьшается; если же этот угол будет меньше 45°, отрезок 1'"7'" увеличивается и становится большой осью эллипса на пл. π3, малой же осью этого эллипса становится отрезок 4"'10"'.
Натуральный вид сечения представляет собой, как уже сказано выше, эллипс. Его оси получаются на чертеже: большая — отрезок 1070 = 1"7", малая — отрезок 40100, равный диаметру цилиндра. Эллипс может быть построен по этим осям.
На рис. 362 показана полная развертка нижней части цилиндра.
Развернутая окружность основания цилиндра разделена на равные между собой части соответственно делениям на рис. 361; отрезки образующих отложены на перпендикулярах, проведенных в точках деления развернутой окружности основания цилиндра. Концы этих отрезков соответствуют точкам эллипса. Поэтому, проведя через них кривую линию, получаем развернутый эллипс (эта линия представляет собой синусоиду) — верхнюю кромку развертки боковой поверхности цилиндра.
К развертке боковой поверхности на рис. 362 присоединены круг основания и эллипс — натуральный вид сечения, что дает возможность сделать модель усеченного цилиндра.
На рис. 363 изображен эллиптический цилиндр с круговым основанием; его ось параллельна пл. π2. Для определения нормального сечения этого цилиндра его надо рассечь плоскостью, перпендикулярной к образующим, в данном случае фронтально-проецирующей плоскостью. Фигура нормального сечения представляет собой эллипс с большой осью, равной отрезку 3070, и с малой, равной 1050 = 1"5".
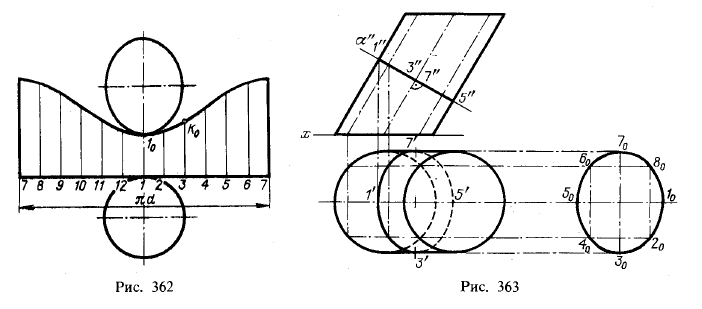
Если надо будет развернуть боковую поверхность данного цилиндра, то, имея нормальное сечение, развертывают ограничивающую его кривую в прямую линию и в соответствующих точках этой прямой, перпендикулярно к ней, откладывают отрезки образующих, беря их с фронтальной проекции. Для разметки образующих делят окружность основания на равные части. При этом и эллипс (нормальное сечение) разделится на такое же число частей, но не все эти части получаются равной
длины. Развертывание эллипса в прямую можно произвести путем последовательного откладывания на прямой достаточно малых частей эллипса.
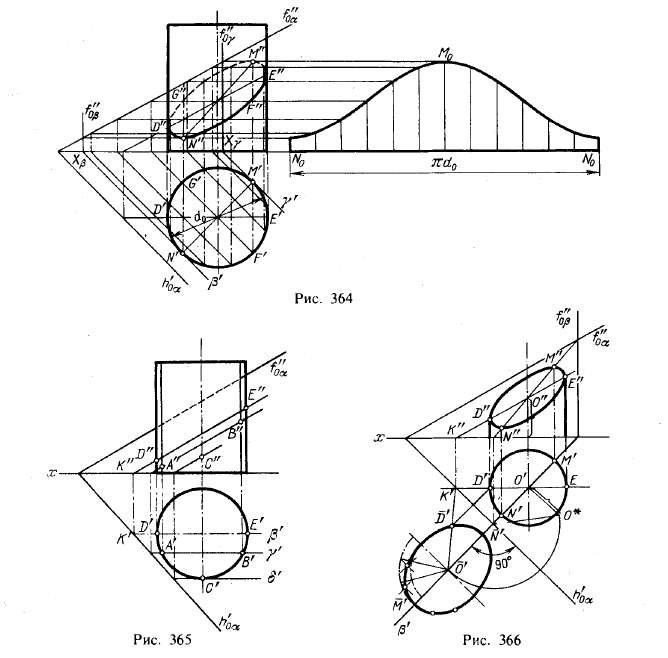
На рис. 364 показан прямой круговой цилиндр, пересеченный плоскостью общего положения. В сечении получается эллипс: секущая плоскость составляет с осью конуса некоторый острый угол.
Подобно тому, как это было на рис. 361, горизонтальная проекция сечения совпадает с горизонтальной проекцией цилиндра. Поэтому положение горизонтальной проекции точки пересечения любой из образующих цилиндра с пл. α известно (например, точка А' на рис. 365). Для нахождения соответствующей фронтальной проекции можно ировести в пл. α горизонталь или фронталь, на которой должна находиться искомая точка. На рис. 365 проведена фронталь; в том месте, где фронтальная проекция фронтали пересекает фронтальную проекцию соответствующей образующей, лежит проекция А". Одна и та же фронталь определяет две точки кривой, А и В (рис. 365). Если же построить фронталь, соответствующую точке С, то
эта линия определит лишь одну точку кривой пересечения. Фронталь, построенная по точкам D и Е, определяет крайние точки D" и Е".
Продолжая аналогичные построения, можно найти достаточно точек для вычерчивания фронтальной проекции линии пересечения.
На рис. 366 верхняя часть цилиндра как бы срезана. Если же фронтальную проекцию показывают полностью, то линию пересечения вычерчивают так, как показано на рис. 364.
На рис. 365 показаны вспомогательные фронтальные плоскости β, γ, δ пересекающие цилиндр по образующим, а пл. α по фронталям. Это соответствует тому, что было сказано в начале параграфа. Вспомогательная пл. δ лишь касается цилиндра, что дает возможность определить только одну точку для кривой.
При построении фронтальной проекции линии пересечения, помимо точек D" и Е" (рис. 365), следует найти еще две крайние точки, а именно М" и N" — наивысшую и наинизшую точки проекции сечения на пл. π2. Для их построения надо выбрать вспомогательную плоскость, перпендикулярную к следу h'0α и проходящую через ось цилиндра (рис. 366). Эта плоскость является общей плоскостью симметрии данных цилиндра и секущей пл. а. Найдя линию пересечения плоскостей α и β, отметим точки М" и N", построив их на фронтальной проекции по точкам М' и N'.
Иной способ нахождения точек М" и N" заключается в проведении двух плоскостей, касательных к цилиндру, горизонтальные следы которых параллельны следу h'0α. Эти плоскости пересекутся с пл. α по горизонталям последней (рис. 364, вспомогательные плоскости β и γ); отметив точки М' и N' построим точки М" и N" на фронтальных проекциях горизонталей.
Отрезок MN представляет собой большую ось эллипса — фигуры сечения данного цилиндра пл. α. Это видно и на рис. 366, где построен в совмещении с пл. π1 эллипс — натуральный вид сечения. Но отрезок M"N" на том же рисунке отнюдь не является большой осью эллипса — фронтальной проекции фигуры сечения. Эту большую ось можно найти по сопряженным диаметрам M"N" и F"G" (рис. 364) построением, указанным в § 21, или специальным построением, приведенным в § 76.
Натуральный вид сечения может быть найден совмещением секущей плоскости с одной из плоскостей проекций, π1 или π2.
На рис. 366 эллипс в совмещенном положении построен по большой и малой осям (там же точка D' получена совмещением фронтали).
Развертка боковой поверхности показана на рис. 364. Обратите внимание на то, что разметка точек — горизонтальных проекций образующих — на окружности основания производилась от точки N'. Этим построение упрощалось, так как с помощью одной и той же горизонтали получаются две точки на фронтальной проек
ции эллипса. Кроме того, фигура развертки имеет ось симметрии. Но при этом точки D' и Е' не попали в число точек, размеченных на окружности.
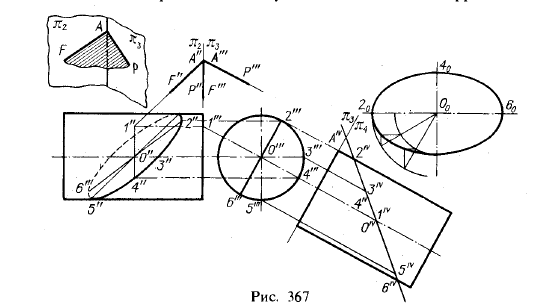
Еще один пример построения фигуры сечения цилиндра вращения плоскостью дан на рис. 367. Это построение выполнено при помощи способа перемены плоскостей проекций. Секущая плоскость задана пересекающимися прямыми — фронталью (AF) и профильной прямой (АР). Так как профильная проекция фронтали и фронтальная проекция профильной прямой лежат на одной прямой А"≡A'", A"'F"' = А"Р", то эти прямые лежат соответственно в плоскостях π2 и π3, (см. рис. 367, слева вверху). Ось π2/π3 проходит через A'"F'"(A"P").
Вводим новую пл. π4 так, что π4⊥π3, и π4⊥АР. Секущая плоскость оказывается перпендикулярной к π4, и проекция на π4 фигуры сечения получается в виде отрезка прямой 2 IV6IV, равного большой оси эллипса — фигуры сечения. Положение прямой AIV6IV определяется построением проекций точек А и 1 на пл. π4.
Проследим построение некоторых точек. Чтобы избежать излишних построений, проекция 1"' была взята на продолжении перпендикуляра, проведенного из О'" на π3/ π4. По точке 1"' была получена проекция 1"; отрезок 1"1"', отложенный от оси π3/π4, определил точку IV и совпадающую с ней точку О1 — проекцию центра эллипса. Зная проекции 0IV и О'", можно получить О" — центр эллипса — искомой фронтальной проекции фигуры сечения.
По точкам 2IV и 2"' найдена точка 2", наименее удаленная от π3, а по точкам 6IV и 6'" - точка 6", наиболее удаленная от π3.
По точке 5"' взяга точка 5IV, и теперь по точкам 5IV и 5"' найдена точка 5"— одна из точек, определяющих разделение эллипса на фронтальной проекции цилиндра на «видимую» и «невидимую» части. Вторая точка расположена симметрично точке 5" по отношению к О".
Остальное ясно из чертежа. Натуральный вид фигуры сечения (эллипс на рис. 367, справа) построен по осям — большой, равной 2IV6IV, и малой, равной диаметру цилиндра.
Вопросы к §§ 55 -56
- Как строится кривая линия при пересечении кривой поверхности плоскостью?
- По каким линиям пересекается цилиндрическая поверхность плоскостью, проведенной параллельно образующей этой поверхности?
- Каким приемом пользуются в общем случае для нахождения точки пересечения кривой линии с плоскостью?
- Какие линии получаются при пересечении цилиндра вращения плоскостями?
- В каком случае эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π1, фронтально-проецирующей плоскостью, спроецируется на пл. π3 в виде окружности?
- Как следует расположить дополнительную плоскость проекций, чтобы эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π1, плоскостью общего положения, составляющей с осью цилиндра угол 45°, спроецировался на эту плоскость проекций в виде окружности?