О проекциях плоских углов
Теория1. Если плоскость, в которой расположен некоторый угол, перпендикулярна к плоскости проекций, то он проецируется на эту плоскость проекций в виде прямой линии.
2.Если плоскость прямого угла не перпендикулярна к плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее в виде прямого же угла.
Положим, что сторона СВ прямого угла АСВ (рис. 89) параллельна плоскости проекций. В таком случае прямая СВ параллельна Ѱ°. Пусть вторая сторона (АС) прямого угла пересекает свою проекцию А°С° в точке К. Проводим в плоскости проекций через точку К прямую параллельно Ѱ°. Прямая KL также параллельпа СВ, и угол CKL получается прямым. Согласно теореме о трех перпендикулярах угол C°KL — также прямой 1). Следовательно, и угол А°С°В° — прямой.
1) Для точек, принадлежащих скрещивающимся прямым и расположенных на одной и той же проецирующей прямой, встречается название «конкурирующие».
Этой теореме о проецировании прямого угла соответствуют две обратные (пп. 3 и 4).
3.Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций.
4.Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой 2 ).
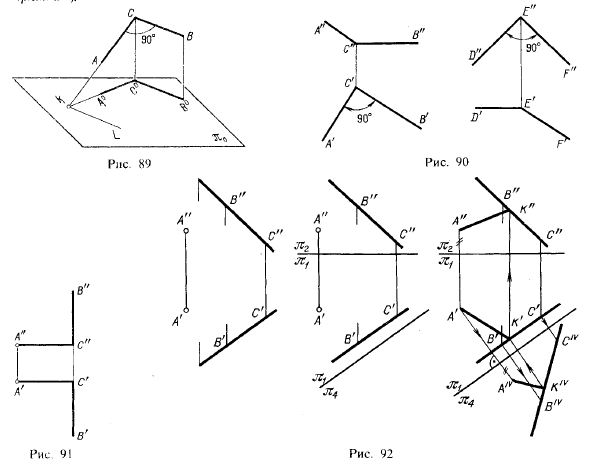
На основании изложенного можно установить, что углы, изображенные на рис. 90, в пространстве прямые.
В каком случае проекции прямого угла на двух плоскостях проекций представляют собой прямые углы? Это бывает, когда одна сторона прямого угла перпендикулярна к третьей плоскости проекций (тогда другая его сторона параллельна згой плоскости), Пример дан на рис. 91: сторона АС перпендикулярна к π3, сторона ВС параллельна π3.
Пользуясь сведениями о проецировании прямого угла, о дополнении системы π1, π2 системой π4, π1 (§ 8) и о расположении проекций прямой, параллельной одной из плоскостей проекций (§ 11), мы можем выполнить следующее построение: провести через некоторую точку А прямую так, чтобы она пересекла данную прямую под-углом 90°, Решение показано на рис, 92, де слева дано исходное положение, в середине показано образование, кроме cистемы 1, π2, еще одной системы π4, π1, причем пл. кπ4||ВС, а справа выполнено построение прямой АК⊥ВС.
1) Согласно прямой теореме о трех перпендикулярах: если КL⊥С°К, то KL.⊥СК. Согласно обратной теореме: если KL⊥СК, то KL⊥С°К.
2) Интересующихся доказательством обратных теорем отсылаем к предыдущим изданиям книги,
Так как пл. π3|| ВС, что обеспечивается проведением оси к pi;4/π1 параллельно В'С', то прямой yгол АКВ (или AKCj проецируется на пл. pi;4 в виде прямого же угла AIVKIVBIV Построив проекции точки А и прямой ВС на пл. pi;4, проводим AIVKIV⊥BIVCIV, а татем получаем проекции К' и К" и проекции А'К' и А"К" (ход построения указан стрелками).
Можно ли считать, что. построив перпендикуляр АК к прямой ВС, мы определили расстояние от А до ВС? Нет, мы только построили проекции отрезка АК; ни одна из них не определяет величины расстояния. Если надо определить величину отрезка АК, т. е. расстояние от А до ВС, то надо продолжить построение, применив хотя бы способ, изложенный в § 13.
5.Если плоскость тупого или острого угла не перпендикулярна к плоскости проекций и хотя бы одна сторона угла параллельна плоскости проекций, то проекция тупого угла на эту плоскость представляет собой тупой угол, а проекция острого угла — острый угол.
Предположим, что прямая СВ (рис. 93) параллельна плоскости проекций. Рассмотрим тупой угол КСВ или острый угол МСВ и проведем в плоскости этою угла прямую CL⊥СВ. Так как угол LCB — прямой, то его проекция — угол LѰ°
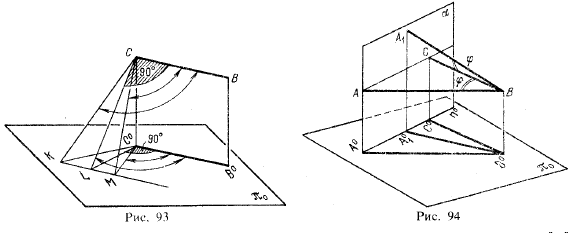
представляет собой также прямой угол. Этот угол заключен внутри угла КѰ° и заключает внутри себя угол МѰ°, следовательно, угол КѰ° — тупой, а угол МѰ° — острый. Таким образом, проекция угла представляет собой угол с тем же названием (прямой, тупой или острый), что и сам угол, если хотя бы одна сторона угла параллельна плоскости проекций. Вообще же проекция любого угла может представлять собой или острый, или прямой, или тупой угол, в зависимости от положения угла относительно плоскости проекций.
6.Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.
Это следует из равенства углов с параллельными и одинаково направленными сторонами.
Поэтому, например, угол между прямой АВ (рис. 50, с. 27) и пл. π2 легко определить: эго — угол между проекцией А'В' и осью х; таким же образом угол между CD и пл. π1 (рис. 51) определится как угол между C"D" и осью х, угол между ЕF (рис. 52) и пл. π2 — как угол между E"'F"' и осью z.
Для прямого угла равенство между его проекцией и самим углом имеет .песта и тогда, когда лишь одна сторона прямого угла параллельна плоскости проекций.
Но для острого или тупого угла, у которого одна сторона параллельна плоскости проекций, проекция угла не может равняться проецируемому углу. При этом проекция острого угла меньше проецируемого угла, а проекция тупого больше проецируемого угла.
Пусть (рис. 94) угол А 1ВС — острый и ею сторона СВ параллельна пл. π0; Ѱ° || СВ. Пл. ?, проведенная через точку С перпендикулярно к СВ, перпендикулярна к пл. π0, пересекая последнюю по прямой n°, проходящей через С° и перпендикулярной к Ѱ°. Если провести через точку В различные прямые под тем же самым острым углом к прямой СВ, то все эти прямые будут пересекать пл. ? в точках, проекции которых расположатся на прямой п°. Положим, что прямые АВ и А1В составляют с прямой СВ равные между собой углы: ∠ АВС = ∠А1ВС. Если при этом АВ параллельна плоскости π0, то ∠ А°В°С° — ∠ АВС. Если же сторона А1В не параллельна π0, то проекция точки ' А1 получится на прямой n° ближе к С°, чем проекция точки А. Следовательно, проекция угла А1ВС представляет собой угол, меньший угла А°В°С°, т. е. ∠А°В°С° < ∠A∠BC.
7.Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.
8.Деление угла в пространстве пополам соответствует делению пополам и его проекции только при условии, что стороны угла составляют с плоскостью проекций равные углы 1 ).
9.Если стороны угла одинаково наклонены к плоскости проекций, то угол-проекция не может равняться проецируемому углу
Это (рис. 95) можно установить путем совмещения угла MKN с пл.π0 при вращении вокруг прямой MN. При этом угол MK°N окажется внутри угла MK1N, а вершины К1 и К° — на общем перпендикуляре к MN.
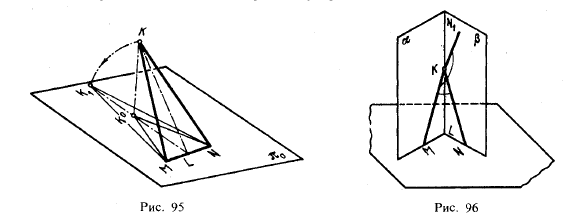
9.Проекции острого и тупого углов могут равняться проецируемому углу не только при условии параллельности сторон угла плоскости проекций.
Из рис. 96 видно, что все углы, например острый угол MKN и тупой угол MKN1, стороны которых соответственно расположены в проецирующих плоскостях ? и ?, имеют своей проекцией угол, равный углу MLN, причем эти углы могут приближаться к 0° и к 180°. Очевидно, среди этих углов может оказаться угол, равный своей проекции.
Пример построения такого угла дан в § 38.
ВОПРОСЫ К §§ 13-15
- Как построить на чертеже прямоугольные треугольники для определения длины отрезка прямой линии общего положения и ее углов с плоскостями проекций π1 и π2?
- Каким условиям должны отвечать углы между прямой общего положения и плоскостями проекций π1 и π2?
- Какое свойство параллельного проецирования относится к параллельным прямым?
- Можно ли по чертежу двух профильных прямых в системе π1,π2 определить, параллельны ли между собой эти прямые?
- Как изображаются в системе π1,π2 две пересекающиеся прямые линии?
- Как следует истолковывать точку пересечения проекций двух скрещивающихся прямых?
- В каком случае прямой угол проецируется в виде прямого угла?
- В каком случае проекция тупого или острого угла обязательно является углом с тем же названием (тупой или острый)?
- Может ли проекция острого или тупого угла, у которого одна сторона параллельна плоскости проекций, равняться самому углу в пространстве?
- В каком случае деление проекции угла пополам соответствует такому делению самого угла в пространстве?
- Может ли угол-проекция на некоторой плоскости проекций равняться проецируемому углу, стороны которого составляют с этой плоскостью равные углы?
- Может ли острый или тупой угол, стороны которого не параллельны плоскости проекций, равняться своей проекции на этой плоскости?