Линия

Линии занимают особое положение в начертательной геометрии. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удается решать многие научные и инженерные задачи, решение которых аналитическим путем часто приводит к использованию чрезвычайно громоздкого математического аппарата.

Линии широко используются при конструировании поверхностей различных технических форм. Умело подбирая линии, дизайнер имеёт возможность придать изящные эстетические формы конструируемым изделиям.

Понятая и определения

В § 8 отмечалось, что при определении геометрических фигур в геометрии принято исходить из основных (неопределяемых) понятий - точка, прямая, плоскость и расстояние, а в современном представлении также понятия множество.

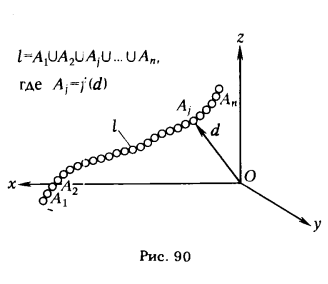
Базируясь на этих элементарных понятиях, линию целесообразно трактовать как траекторию перемещения точки (рис. 90). Такое представление линии позволяет получить определение линии, используя такие основные понятия геометрии, как точка и множество. В этом случае линию можно рассматривать как непрерывное множество всех принадлежащих ей точек.

Если учесть, что положение точки при ее движении по заданной траектории будет зависеть от непрерывно меняющейся величины d (расстояние до точки от начала координат*), то можно утверждать, что положение точки, принадлежащей линии, определяется непрерывно меняющейся величиной d. Тогда, окончательно приняв d за параметр, приходим к следующему определению - линия есть непрерывное однопараметрическое множество точек.

В этом определении словом непрерывное подчеркивается, что двум бесконечно близким значениям параметра соответствуют две также бесконечно близкие точки.

Следует иметь в виду, что данное определение линии является условным. В действительности положение точки будет зависеть не только от вектора d (определяющего величину расстояния) , но и от углов его наклона к плоскостям проекций.

Мы останавливаемся на нем лишь потому, что в дальнейшем, при изложении гл. IV "Поверхность", оно позволяет получить определение поверхности, основание также на понятиях точка и множество и, что более важно, подойти к этому определению с точки зрения кинематического способа получения поверхности.

* В случае окружности начало координат не должно совпадать с ее центром.

Рассматривая поверхность как след, который оставляет геометрическая фигура при своем перемещении в пространстве, можно ввести понятие определитель, которое играет весьма важную роль в теории поверхностей.

Линии подразделяются на алгебраические*, если в декартовой системе координат они определяются алгебраическими уравнениями, и трансцендентные**, если они описываются трансцендентными уравнениями.

Линии могут быть пространственными и плоскими.

Пространственными или линиями двоякой кривизны называют линии, все точки которых не принадлежат одной плоскости.

Линии, у которых все точки принадлежат одной плоскости, называют плоскими.

Если алге6раическое уравнение, описывающее линию, n-й степени, то алгебраическая кривая считается n-го порядка. Порядок алгебраической кривой определяется также числом точек ее пересечения с плоскостью (для пространственной линии) или прямой (для плоской линии). При этом следует иметь в виду, что в число точек пересечения включаются точки с действительными и мнимыми координатами.

Простейшей линией является прямая. Так как свойства прямой и задание ее на эпюре Монжа уже известны читателю (см. гл. I, § 8), в настоящей главе речь будет идти о характеристиках и свойствах кривых линий (пространственных и плоских) и построении их ортогональных проекций.

I. Пространственные кривые линии

Было отмечено, что пространственными кривыми называются линии, все точки которых не принадлежат одной плоскости. Рис. 91 дает наглядное представление о произвольной пространственной кривой линии.

• Касательные и нормали к пространственной кривой

  На рис. 92 показана пространственная кривая l. Возьмем на ней произвольную точку М и проведем через нее секущие [МА) и [МВ).Подробнее

• Приближенные способы построения касательной и нормали к плоской кривой

  Графический способ построения касательной и нормали к плоской кривой базируется на использовании "кривой ошибок".Подробнее

• Кривизна плоской кривой

  Величина угла α° между полукасательными в двух бесконечно близких точках, отнесенная к длине дуги s, заключенной между этими точками, характеризует степень искривленности кривой линии.Подробнее

• Приближенный способ построения центра кривизны кривой в заданной топке

  Из рис. 100 видно, что окружность кривизны в точке соприкасания имеет общую с кривой l касательную tA и нормаль nA. Этим свойством можно воспользоваться для графического определения центра кривизны кривой в данной точке.Подробнее

• Эволюта и эвольвента

  Определение эволюты и эвольвенты неразрывно связано с понятием кривизны кривой линии. Если определить положение центров кривизны O1, O2, ... , Оn ряда, принадлежащих данной кривой l (рис. 102), точек А1, А2, ... , Аn и соединить их плавной кривой, то получим кривую m, называемую эволютой кривой l. Итак, эволюта есть множество точек, являющихся центрами кривизны линии.Подробнее

• Классификация точек плоской кривой

  Вид кривой l вблизи некоторой точки М с единственной касательной t зависит от характера движения точки вдоль касательной и направления: поворота касательной. Поясним это утверждение на примерах.Подробнее

• Ортогональные проекции линии

  Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить между собой одноименные проекции в той же последовательности, в какой они располагались на оригинале.Подробнее

• Определение длины пространственной кривой по её ортогональным проекциям

  На рис. 114 даны две проекции пространственной кривой l. Чтобы определить длину кривой, необходимо осуществить ее спрямление. Спрямление пространственной кривой, заданной ортогональными проекциями, осуществляется следующим путем:Подробнее