Неопределяемые понятия геометрии; ортогональные проекции точки, прямой, плоскости
ТеорияК основным - неопределяемым - понятиям геометрии относятся: точка, прямая, плоскость, расстояние и множество; они не могут быть определены с помощью других, более простых (элементарных) понятий.
В то же время с помощью системы аксиом возможно установить отношения между отмеченными основными понятиями, которые в дальнейшем служат основанием для формулировки различных геометрических предложений (теорем), составляющих теоретическую базу геометрии. Учитывая особую роль, которую играют в геометрии, в том числе и геометрии начертательной, основные понятия, целесообразно начать изложение курса начертательной геометрии, связанного с использованием метода проецирования, с рассмотрения ортогональных проекций точки, прямой, плоскости и определения длины отрезка прямой (являющегося мерой расстояния), заданного ортогональными проекциями *.
По этой же причине проекции точки, прямой, плоскости и определение длины: отрезка прямой рассматриваются вместе, несмотря на
* Рассмотрение проекций множества теряет всякий смысл, так как в геометрии имеют дело с множествами, элементами которых являются точки. В общем случае множество не имеет границ - оно представляет собой пространство, заполненное точками. Проекция такого множества покроет все поле проекции. Поэтому речь может идти только о проекциях конечного множества, образующего конкретную геометрическую фигуру.
то, что прямая относится к разделу линия, плоскость является представителем поверхностей, о которых речь будет идти позже, в гл. III и IV, а определение расстояния составляет содержание § 55 гл. VI.
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ
Точка, как математическое понятие, не имеет размеров. Очевидно, если объект проецирования является нульмерным образом, то говорить о его проецировании бессмысленно.
В геометрии под точкой целесообразно понимать физический объект, имеющий линейные измерения. Условно за точку можно принять шарик с бесконечно малым радиусом. При такой трактовке понятия точки можно говорить о ее проекциях. Более того становится оправданным сделанное ранее (см. с. 13) определение геометрической фигуры как множества всех принадлежащих ей точек.
При построении ортогональных проекций точки следует руководствоваться первым инвариантным свойством ортогонального проецирования А → А'.
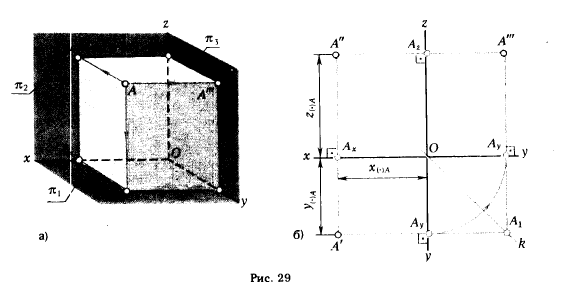
Пусть даны в пространстве точка А и три взаимно перпендикулярные плоскости проекции (рис. 29,а). Положение точки в пространстве определяется тремя координатами (x, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку А провести прямые, перпендикулярные к плоскостям проекций, определить точки А', А", А"' встречи этих прямых с плоскостями проекций и измерить величины отрезков [АА'], [АА"], [АА'"], которые укажут соответственно значения аппликаты z, ординаты у и абсциссы х точки А.
Точки А', А", А"' называют ортогональными проекциями точки А, при этом согласно принятым обозначениям (см. с. 9) : А' - горизонтальная проекция точки А; А" - фронтальная проекция точки А; А"' - профильная проекция точки А. Отрезки: [АА"'] ≅ [ОАx] - абсцисса точки А; [АА"] ≅ [ОАy] - ордината точки А; [АА' ] ≅ [OAz] - аппликата точки А.*
* Конгруентность отрезков [АА"'] ≅ [ОАx], [АА"] ≅ [ОАy], [АА' ] ≅ [0Az] следует из того, что параллелепипед AA"AzA"' А'АxОАy прямоугольный.
Прямые (АА'), (АА"), (АА'") называются проецирующими прямыми.
При этом прямую (АА'), проецирующую точку А на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой.
Аналогично: прямые (АА") и (АА'") называют соответственно: фронтально (АА") и профильно (АА'") проецирующими прямыми.
Две проецирующие прямые, проходящие через точку А, определяют плоскость, которую принято называть проецирующей.
Чтобы получить эпюр точки А, преобразуем пространственный макет, изображенный на рис. 29,а, так, как это было показано в предыдущем параграфе (см. рис. 26 и 27).
Фронтальная проекция точки А остается на месте, как принадлежащая плоскости π2, которая не меняет своего положения при рассматриваемом преобразовании.
Горизонтальная проекция А' вместе с горизонтальной плоскостью проекции повернется по направлению движения часовой стрелки и расположится на одном перпендикуляре к оси х с фронтальной проекцией А".
Профильная проекция А'" будет вращаться вместе с профильной плоскостью проекции и к концу преобразования займет положение, указанное на рис. 29,6. При этом А'" будет принадлежать перпендикуляру к оси z, проведенному через А", и будет удалена от оси z на такое же расстояние, на какое горизонтальная проекция А' удалена от оси х.
Поэтому связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [А'Аy] и [АyА'") и сопрягающей их дуги окружности с центром в точке пересечения осей х, у, z. Отмеченной связью пользуются для нахождения недостающей профильной (или горизонтальной) проекции.
Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями может быть установлена с помощью ломаной линии А'А1 А"' с вершиной А1 на биссектрисе угла, образованного осями у, принадлежащими плоскостям π1 и π3.
Биссектрису ОА1 называют постоянной прямой k эпюра Монжа.
Чтобы определить положение точки А в пространстве, необходимо знать три ее координаты (х, у, z), равные длинам отрезков [АА'"], [АА"], [АА'] (см. рис. 29,а). Величины этих отрезков могут быть легко определены на эпюре рис. 29,6:
[АА"'] ≅ [А'Аy] ≅ [А"Аz];
[АА"] ≅ [А'Аx] ≅ [A'"Az];
[АА'] ≅ [А"Аx] ≅ [А"'Аy].
Попутно отметим, что горизонтальная проекция точки А определяется абсциссой х и ординатой у; ее фронтальная проекция - абсциссой х и аппликатой z, а профильная проекция - ординатой у и аппликатой z, т. е.

Из записи (1) следует:
1. Точка в пространстве удалена:
а) от плоскости проекции π3 на такую же величину, на какую горизонтальная проекция этой точки А' удалена от оси у(или же фронтальная проекция А" от оси z);
б) от плоскости проекции на такую же величину, на какую горизонтальная проекция этой точки А' удалена от оси х (или ее профильная проекция А"' от оси z);
в) от плоскости проекции π1 на такую же величину, на какую ее фронтальная проекция А" удалена от оси х (или ее профильная проекция А'" удалена от оси у).
2. Две проекции любой точки принадлежат одному перпендикуляру (одной линии связи):
а) горизонтальная и фронтальная - перпендикуляру к оси x;
б) горизонтальная и профильная - перпендикуляру к оси у;
в) фронтальная и профильная - перпендикуляру к оси z.
3. Для ортогонального проецирования отмеченное ранее свойство (см. с. 19) может быть сформулировано: положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Как следствие из этого - по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью ортогональную проекцию.
Действительно, сочетание любых двух ортогональных проекций точки всегда дает нам значения всех трех ее координат.
Пользуясь табл. 1, помещенной в § 7, и зная положительное и отрицательное направление осей, а также принимая во внимание свойства проекций точки (пп. 1, 2, 3), можно указать на эпюре проекции точки, если известны ее координаты, или определить, в каком октанте расположена точка и на какие расстояния она удалена от плоскостей проекций, если заданы хотя бы две ее ортогональные проекции.
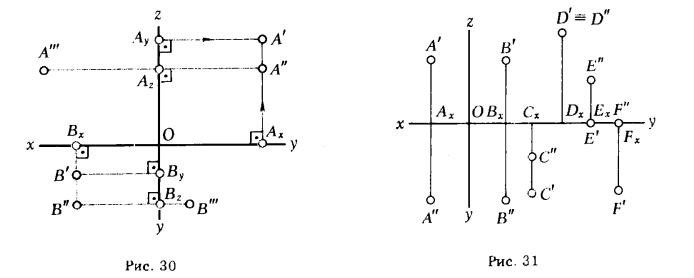
ПРИМЕР. Даны координаты точек А (-20, -20, +15) и В (+15, +5, -10). Требуется найти положение проекций этих точек и определить, в каких октантах они находятся (рис. 30).
Для определения положения горизонтальной проекции А' точки А откладываем от начала координат на отрица тельном направлении оси х (от точки О вправо) значение х = - 20 мм и определяем точку Ах, а на отрицательном направлении оси у откладываем значение у = - 20 (.для плоскости π1 отрицательное направление оси у совпадает с положительным направлением оси z) и определяем положение точки Аy.
Пересечение перпендикуляров, восставленных из точек Аx и Аy к соответствующим осям х и у, укажет положение горизонтальной проекции А' точки А.
Мы знаем, что фронтальная А" и горизонтальная А' проекции точки принадлежат одному перпендикуляру к оси х (см. п. 2, с. 22) и то, что фронтальная проекция удалена от оси х на величину аппликаты z (в данном случае z = +15). Поэтому для определения положения А" откладываем от точки Аx на перпендикуляре к оси х значение аппликаты z = + 15.
Аналогично находим положение горизонтальной и фронтальной проекций точки В. Для этого на положительных направлениях осей х и у откладываем соответственно 15 и 5 мм. Эти координаты определяют положение В . Фронтальная проекция принадлежит прямой линии связи, проходящей через В' перпендикулярно к оси х, и удалена от этой оси на заданное значение z = - 10.
Приведенная в § 7 табл. 1 знаков координат точек, расположенных в разных октантах, позволяет легко определять, какому октанту принадлежит точка, если известны хотя бы две ее проекции.
Точка А находится в VI октанте пространства, так как она располагается за фронтальной плоскостью проекции (в зоне отрицательных значений ординаты у) выше горизонтальной (аппликата z - положительна) и правее профильной плоскости проекции (абсцисса х - отрицательна) , т. е. в части пространства, ограниченной верхней правой полой плоскости π2, задней правой полой плоскости π1 и задней верхней полой профильной плоскости проекции π3
Чтобы найти профильную проекцию точки, достаточно из А" провести пря-
мую, перпендикулярна к оси z, и отложить на ней от этой оси влево (по отрицательному направлению оси у, принадлежащей профильной плоскости проекции) значение у = -20 мм.
Точка В расположена в IV октанте, в котором координаты х и у - положительны, а координата z - отрицательна. На рис. 30 указано также положение профильной В"' проекции этой точки.
Нa рис. 31 показаны горизонтальные и фронтальные проекции точек А, В, С, D, Е, F. Зная положительные и отрицательные направления осей, можно без труда определить октант, которому принадлежит точка; так, точка А находится в третьем октанте пространства, а точка В, симметричная точке А относительно плоскости π3, принадлежит седьмому октанту. Точка С находится в восьмом октанте, так как значения абсциссы х и аппликаты z - отрицательны, а значение ординаты у - положительно.
На рис. 31 показаны проекции D' и D" точки D. Для этой точки характерно равенство аппликаты z и ординаты у, поэтому точка D удалена на одинаковое расстояние от плоскостей π1 и π2(|D'Dx| = |D"Dx|), т. е. она принадлежит биссекторной плоскости шестого и восьмого октантов. На рис. 31 указаны также проекции точек Е и F. Точка Е принадлежит фронтальной плоскости проекции π2 (ордината У(·)Е = 0). а точка F - горизонтальной плоскости проекции π1 (z (·)F=0).
В тех случаях, когда нет необходимости в определении положения точки (или любой геометрической фигуры) относительно системы плоскостей проекций, можно не указывать на эпюре осей проекций. Иными словами, для безосного чертежа плоскости проекции принимаются неопределенными до параллельного переноса (т. е. могут перемещаться параллельно самим себе).
В инженерной практике при Составлении чертежей, когда требуется определить (форму и размеры геометрической фигуры или взаимное расположение совокупности геометрических фигур, обычно оси проекций не указывают. Отсутствие на чертеже осей не мешает определять третью проекцию любой точки по двум ее заданным проекциям, если указаны три проекции какой-либо другой точки.
ПРИМЕР. Даны три проекции точки А (А', А", А"' ), а также горизонтальная и фронтальная проекции точки В (В' и В"). Требуется найти профильную проекцию В'" (рис. 32). Через горизонтальную проекцию точки А проводим прямую, параллельную линии связи (А" А"') , а через профильную проекцию А'" проводим прямую, параллельную линии связи (А'А") , и отмечаем точку их пересечения A1 . Через точку А1 проводим постоянную прямую k. Прямая k проводится как биссектриса угла А'A1 А"'.
Зная положение постоянной прямой, легко найти недостающую профильную
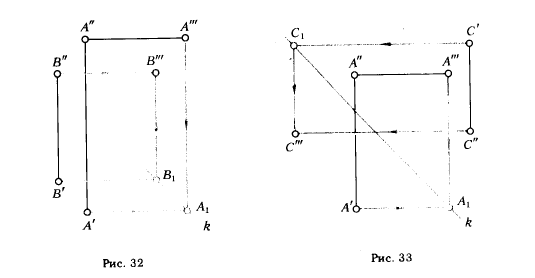
проекцию точки В. Для этого через В' проводим горизонтальную прямую, отмечаем точку В1 ее пересечения с постоянной прямой k. Через точку В1 проводим вертикальную прямую. Точка ее пересечения с горизонтальной прямой, проведенной через В", определяет искомую профильную проекцию В"'.
Постоянная прямая позволяет решать задачу по определению третьей проекции точки по двум заданным независимо от того, в каком октанте находится точка.
ПРИМЕР. Даны три проекции точки А (А', А", А"'), а также горизонтальная и фронтальная проекции точки С (С' и С"), расположенной в VI октанте (рис. 33). Требуется определить С"'.
Через данную проекцию А' проводим горизонтальную прямую и отмечаем точку пересечения ее с вертикальной прямой, проведенной через А'". Через точку A1 проводим постоянную пря мую k.
Для определения третьей проекции точки С достаточно через точку С провести горизонтальную прямую, а из точки C1 пересечения ее с постоянной прямой k - вертикальную прямую. Точка пересечения этой вертикали с горизонтальной прямой, проведенной через С", укажет положение искомой проекции С"'. Если на безосном чертеже потребуется указать оси, то это всегда можно сделать (с точностью до параллельного переноса). Для этого одну из осей, например х, проводим произвольно, следя лишь за тем, чтобы она была перпендикулярна линии связи, соединяющей горизонтальную и фронтальную проекции точки. Тогда ось z определится как прямая, перпендикулярная к оси х в точке пересечения оси х с постоянной прямой k.
ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ
При построении проекции прямой следует исходить из инвариантного свойства 1а (см. § 6) ортогонального проецирования:
При ортогональном проецировании на плоскость прямая, не перпендикулярная плоскости проекции, проецируется в прямую.
Поэтому для определения проекции прямой достаточно знать проекции двух не тождественных точек, принадлежащих этой прямой.
[АВ], определяющий прямую l (рис. 34,а), занимает произвольное (общее) положение по отношению к плоскостям проекций (углы наклона прямой l к плоскостям проекций - произвольные, но отличные от 0 и 90°). Такая прямая называется прямой общего положения.
* Естественно, будут справедливы и следующие утверждения:
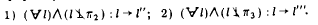
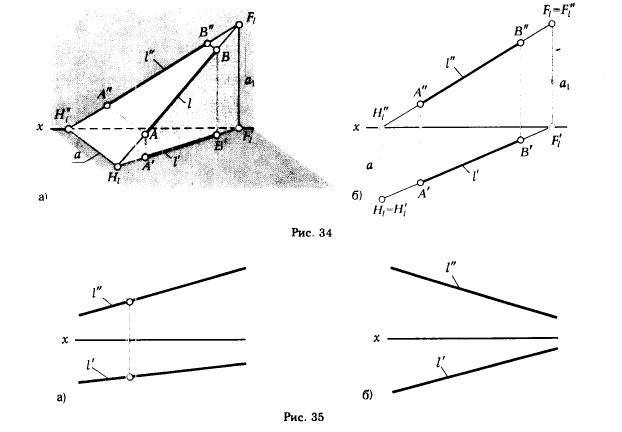
На эпюре проекции прямой общего положения составляют с осями проекций также произвольные углы (рис. 34,6). Прямую на эпюре можно задать не только проекциями ее отрезка (см. рис. 34,6), но и проекциями некоторой произвольной части прямой, не указывая концевых точек этой части. При этом можно ограничиться обозначением проекции только одной буквой, отнеся ее к какой-либо точке прямой (рис. 35,а) или к прямой (точнее ее проекции) в целом (рис. 35,6).
Прямая общего положения пересекает все основные плоскости проекции. Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой.
В зависимости от того, с какой плоскостью проекции происходит встреча прямой l, следы обозначают и называют: Hl - горизонтальный след прямой l; Fl - фронтальный след прямой l. H'l, H"l, F'l, F"l - соответственно горизонтальная и фронтальная проекции следов Hl и Fl Следует иметь в виду, что Hl ≡ Н'l;Fl ≡ F"l.
Установим правило нахождения следов прямой. Для примера рассмотрим определение Hl (см. рис. 34,6). Горизонтальный след - точка, принадлежащая как прямой l, так и плоскости проекции π1(Hl = l ∩ π1 ),поэтому H"l ∈ l" и H"l isin; х, следовательно, H"l = l" ∩ х. Горизонтальная проекция Н'l ∈ l' (так как Нl ∈ l). Поэтому для нахождения горизонтального следа прямой необходимо:
1) отметить точку пересечения фронтальной проекции прямой с осью х (l" ∩ х = Н"l);
2) через полученную точку провести прямую а, перпендикулярную оси х(а ⊥ х)
3) пересечение перпендикуляра а с горизонтальной проекцией прямой укажет положение горизонтального следа Hl = (a ∩ l' = H1).
Таким образом, алгоритм определения горизонтального следа прямой l может быть записан: H1 = (l" ∩ х = Н"1); (а ⊥ х, а ∋ H"1); а ∩ l'.
Для определения фронтального следа прямой вместо l" ∩ х выполняется операция l' ∩ х = F'1, а прямая а1 ⊥ х проводится через точку F'1. Последняя операция заключается в нахождении F"1 = а1 ∩ l"
Частные случаи расположения прямой
Кроме рассмотренного общего случая (см. рис. 34,а, б), существуют следующие частные случаи расположения прямой по отношению к заданной системе плоскостей проекций:
А. Прямая параллельна плоскости проекции.
Б. Прямая перпендикулярна плоскости проекции.
В. Прямая принадлежит плоскости проекции (частный случай параллельности) .
Рассмотрим каждый из этих случаев.
А. Прямая, параллельная плоскости проекции (горизонталь, фронталь)*.
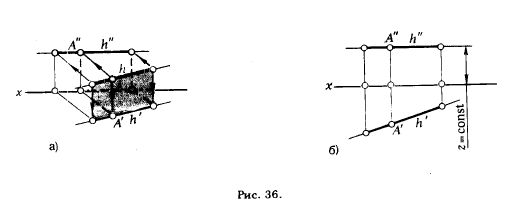
1. Горизонталь - прямая, параллельная горизонтальной плоскости проекции: h || π1.
Все точки горизонтали удалены на одинаковые расстояния от плоскости π1. Поэтому фронтальная проекция любой горизонтали параллельна оси х. Горизонтальная проекция может занимать любое положение (рис. 36,а и б) . ∀A ∈ h; z(·) A - const, поэтому h" || х.
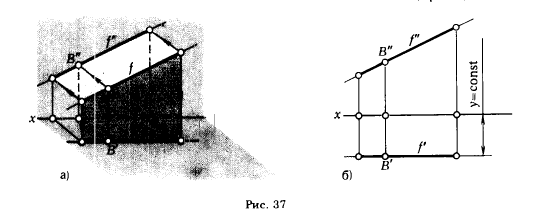
2. Фронталь - прямая, параллельная фронтальной плоскости проекции: f||π2.
Все точки фронтали удалены на одинаковое расстояние от фронтальной плоскости π2. Поэтому горизонтальная проекция любой фронтали параллельна оси х. Фронтальная проекция может занимать любое положение (рис. 37,а иб). ∀B ∈ f; y(·) B - const, поэтому f' || х.
Б. Прямая, перпендикулярная плоскости проекции (проецирующая прямая).
* Горизонталь и фронталь называют также линиями уровня.
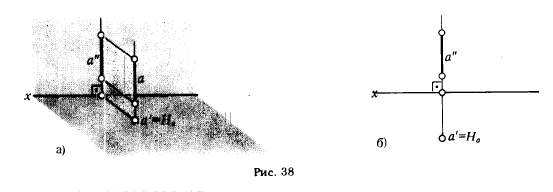
1. Горизонтально проецирующая прямая - прямая, перпендикулярная горизонтальной плоскости проекции: a ⊥ π1.
Такая прямая проецируется на плоскость π1 в точку; ее фронтальная проекция перпендикулярна оси х (рис. 38,а и б) : а' - точка, а" - прямая ⊥ х.
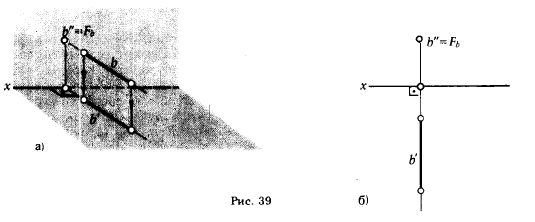
2. Фронтально проецирующая прямая - прямая, перпендикулярная фронтсигьной плоскости проекции: b ⊥ π2.
Эта прямая проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси х (рис. 39,а и б): b" - точка, b' - прямая ⊥ х. Прямые а и b являются частными случаями соответственно фронтали и горизонтали.
В. Прямая, принадлежащая плоскости проекции.
Характерным признаком для эпюра, на котором изображена такая прямат, будет принадлежность одной из проекций прямой оси.
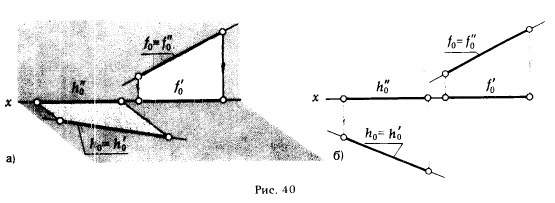
На рис. 40,а и б показаны проекции прямых h0 и f0. Прямая h0 принадлежит горизонтальной плоскости проекции: h0 ⊂ π1. Прямая f0 принадлежит фронтальной плоскости проекции: f0 ⊂ π2. Прямые h0 и f0 являются нулевыми горизонталью и фронталью.
ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ ПЛОСКОСТИ
Плоскость является простейшей поверхностью. Положение плоскости в пространстве однозначно определяется тремя различными точками А, В, С, не принадлежащими одной прямой. Поэтому для задания плоскости на эпюре Монжа достаточно указать проекции:
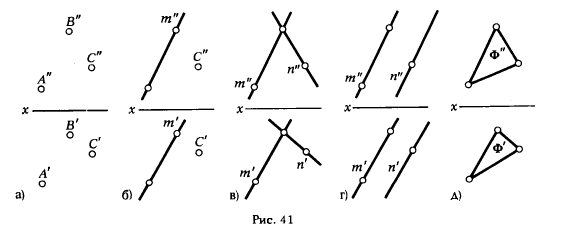
а) трех различных, не принадлежащих одной прямой точек (рис. 41,с);
б) прямой и не принадлежащей ей точки (рис. 41,6);
в) двух прямых, пересекающихся в собственной (рис. 41,в) ИЛИ несобственной (рис. 41,г) точке.
Плоскость может быть задана также проекциями отсека плоской фигуры Ф (рис. 41,6). В некоторых случаях бывает целесообразным задавать плоскость не произвольными пересекающимися прямыми, а прямыми, по которым эта плоскость пересекает плоскости проекции. Такой вариант задания плоскости называют заданием плоскости следами. На рис. 42;,а показана плоскость а. Эта плоскость пересекает ось проекции в точке Хα, а плоскости проекции по прямым h0α, f0α. Прямую, по которой плоскость пересекает плоскость проекции, называют следом плоскости. При этом различают:
h0α = α ∩ π1 -горизонтальный след плоскости α;
f0α = α ∩ π2 -фронтальный след плоскости α.
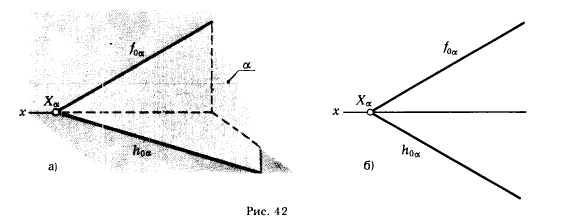
Точку Хα = х ∩ α пересечения оси x с плоскостью α называют точкой схода следов (в этой точке сходятся два следа).
На рис. 42,б показано задание плоскости следами. Сопоставляя между собой наглядное изображение (рис. 42,а) и его плоскостную модель - эпюр Монжа (рис. 42,6), мы видим, что задание плоскости следами обладает преимуществом перед другими вариантами ее изображения на эпюре:
во-первых, сохраняется наглядность изображения, что позволяет легко представить положение плоскости в пространстве;
во-вторых, при задании плоскости следами требуется указать только две прямые вместо четырех (см. рис. 41,в, г) или шести (см. рис. 41,6).
Показанная на рис. 42 плоскость α занимает общее (произвольное) положение по отношению к плоскостям проекций (углы наклона этой плоскости к плоскостям проекций - произвольные, но отличные от 0 и 90° ). Такая плоскость называется плоскостью общего положения.
Из рис. 42,6 видно, что на эпюре Монжа следы плоскости общего положения составляют с осью проекции также произвольные углы.
Частные случаи расположения плоскости
Кроме рассмотренного общего случая (см. рис. 42), плоскость по отношению к плоскостям проекций может занимать следующие частные положения:
А. Перпендикулярное к плоскости проекции.
Б. Параллельное плоскости проекции.
Рассмотрим эти случаи.
А. Плоскость, перпендикулярная к плоскости проекции. Такие плоскости называют проецирующими, при этом различают:
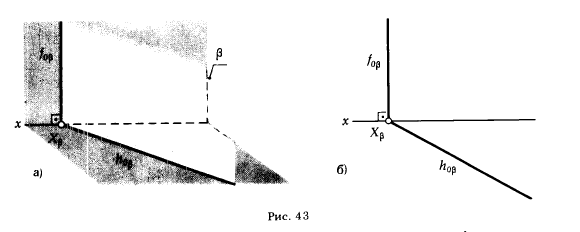
1. Горизонтально проецирующую плоскость β ⊥ π1.
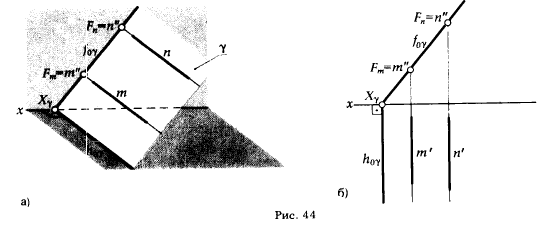
2. Фронтально проецирующую плоскость γ ⊥ π2.
Рис. 43, 44 дают наглядное представление о проецирующих плоскостях и их задании на эпюре Монжа, причем плоскость β задана следами, γ - параллельными прямыми (m и n).
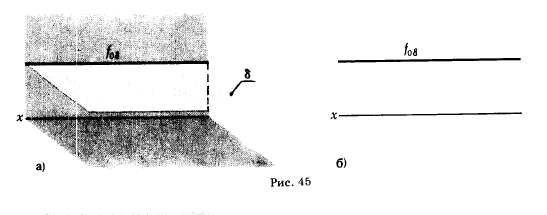
Б .Плоскость, параллельная плоскости проекции.
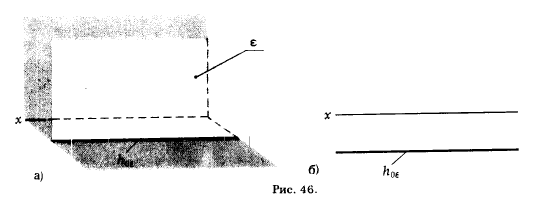
Эти плоскости называют плоскостями уровня, причем плоскость δ || π1 называют горизонтальной, а плоскость ε || π2 - фронтальной. Рис. 45,а дает предстгшление о горизонтальной плоскости δ , а на рис. 46,а показана фронтальная плоскость ε. На рис. 45,б и 46,б эти плоскости заданы на эпюре Монжа.
Главные линии плоскости
Главными линиями плоскости называют:
1. Горизонталь - прямую, принадлежащую плоскости и параллельную горизонтальной плоскости проекции.
2. Фронталь - прямую, принадлежащую плоскости и параллельную фронтальной плоскости проекции.
3. Линию наибольшего наклона - прямую, принадлежащую плоскости и перпендикулярную к горизонтали или фронтали этой плоскости.
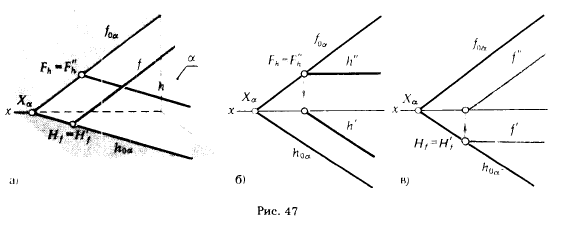
На рис. 47,а показаны горизонталь h и фронталь f плоскости α. Рис. 47,б и в иллюстрируют задание этих линий на эпюре Монжа. Из рис. 47,б, в видно, что горизонталь плоскости параллельна ее горизонтальному, а фронталь - фронтальному следу.
Характерные особенности проекций горизонтали и фронтали приведены ниже:
Проекция:
горизонтальная фронтальная
Горизонталь.............Параллельна h0α Параллельна оси х
Фронталь.................Параллельна оси х Параллельна f0α
Представление о линии наибольшего наклона плоскости дает рис. 48, на котором показана прямая с - линия наибольшего наклона плоскости α к горизонтальной плоскости проекции. В некоторых учебниках ее называют также линией наибольшего ската.
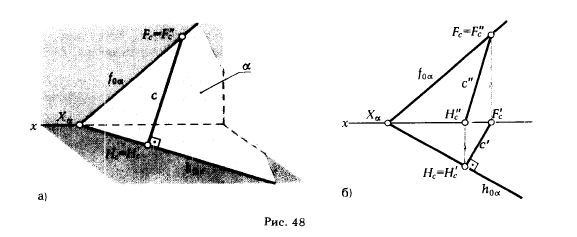
Отличительной особенностью линии наибольшего наклона прямой к плоскости π1 является перпендикулярность ее горизонтальной проекции горизонтали h' плоскости α или ее горизонтальному следу h0α.
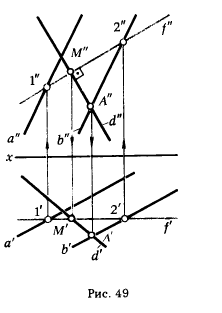
У прямой d - линии наибольшего наклона плоскости α к плоскости проекции π2 - фронтальная проекция перпендикулярна фронтальной проекции фронтали плоскости f' или ее фронтальному следу f0α. Рис. 48,а х показывает прямую с - линию наибольшего ската плоскости α; на рис. 48,6 эта линия задана на эпюре Монжа. На рис. 49 показана прямая d - линия наибольшего наклона плоскости β (а || b) к плоскости проекции π2.Так как плоскость β задана параллельными прямыми и направление фронтального следа плоскости f0β нам не известно, то для определения направления фронтальной проекции прямой d необходимо построить фронтальный след плоскости f0β или фронтальную проекцию фронтали этой плоскости.
На рис. 49 проведена фронталь f (f', f") плоскости β (ее построение проще, чем определение фронтального следа плоскости β). Затем через произвольную точку А" (А ∈ β) проведена фронтальная проекция d" (d" ⊥ f"). Отмечена точка М" = d" ∩ f". По А" и М" найдены А' и М'. Эти две точки указывают положение горизонтальной проекции прямой d' - линии наибольшего наклона плоскости β к плоскости проекции π2 .
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ
Расстояние между двумя точками А и В определяется длиной отрезка прямой, заключенного между этими точками.
Из инвариантных свойств ортогонального проецирования следует, что ортогональная проекция отрезка будет конгруентна оригиналу лишь в том случае, когда он параллелен плоскости проекции (см. § 6, свойство 2д) :
([АВ] || π1)⇔[А'В']≅[АВ].
Аналогично:
([АВ] || π2)⇔[А"В"]≅[АВ].
Во всех остальных случаях отрезок проецируется на плоскость проекции с искажением. При этом ортогональная проекция отрезка всегда будет меньше его длины.
Для установления зависимости между длиной отрезка прямой и длиной его проекций рассмотрим рис. 50,а. В прямоугольной трапеции АВВ'А' (углы при вершинах А' и В' - прямые) боковыми сторонами являются отрезок АВ и его горизонтальная проекция А'В', а основаниями - отрезки А А' и ВВ', по величине равные удалениям концов А и В отрезка от горизонтальной плоскости проекции π1.
Проводим в плоскости трапеции АВВ'А' через точку А прямую АВ1, параллельную горизонтальной проекции отрезка АВ. Получим прямоугольный треугольник АBВ1, у которого катет АВ1≅А'В', а катет ВВ1 равен разности аппликат концов отрезка (|ВВ'| - |АА'|). Гипо
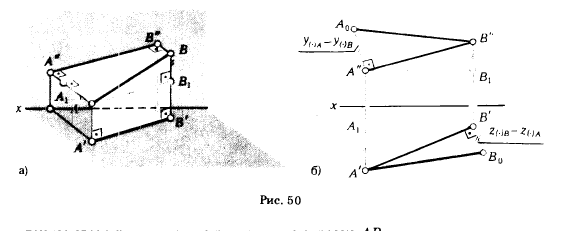
тенуза этого треугольника равна длине отрезка АВ.
|АВ|2 = |А'В'|2 + (|ВВ'|- |AA'|)2.
Зависимость между длиной отрезка и его фронтальной проекцией может быть установлена с помощью треугольника AA1B, в котором гипотенуза равна длине отрезка, один из катетов - фронтальной проекции отрезка, а другой - разности удалений концов отрезка от фронтальной плоскости проекции:
|АВ|2 = |А"В"|2 + (|АА"|- |ВВ"|)2.
Приведенные примеры показывают, что для графического определения на эпюре Монжа длины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную) проекцию отрезка, а за другой катет - разность удалений концов отрезка от горизонтальной (фронтальной) проекции.
На рис. 50,б показано определение действительной величины отрезка АВ с помощью построения треугольника А'В'В0. На этом же чертеже приведен второй вариант решения задачи - путем построения треугольника А"В"А0 на базе фронтальной проекции отрезка.
Построение прямоугольного треугольника не единственный графический способ определения длины отрезка. В дальнейшем будут показаны различные способы преобразования ортогональных проекций, с помощью которых можно получить более экономичные решения.
С помощью прямоугольного треугольника можно решать задачу на построение на эпюре проекции отрезка наперед заданной длины.
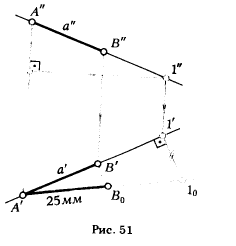
ПРИМЕР. На прямой общего положения a отложить от точки А вправо отрезок длиной 25 мм (рис. 51).
РЕШЕНИЕ:
1. Отмечаем на прямой a произвольную точку 1 (1', 1");
2. Определяем длину отрезка [А1];
3. На прямой (A'l0) от точки А откладываем отрезок А'В0 длиной 25 мм.
4. Из точки В0 опускаем перпендикуляр на прямую а'. [АВ'| является горизонтальной проекцией отрезка заданной длины.
При последующем изложении материала нам часто придется обращаться к параллельным прямым и плоскостям. В связи с этим целесообразно не только показать задание на эпюре Монжа точки, прямой, плоскости, но и выяснить условия, которые должны быть выполнены для изображения параллельных прямых, плоскостей, прямой и плоскости.
В расширенном евклидовом пространстве (пространстве, дополненном несобственными точками и прямыми) две прямые, прямая и плоскость, две плоскости всегда пересекаются. Различие по сравнению с обычным евклидовым пространством состоит лишь в том, что точка пересечения прямых или прямой и плоскости и прямая, являющаяся результатом пересечения двух плоскостей, могут быть как собственными, так и несобственными. В последнем случае прямые, прямая и плоскость, плоскости считаются параллельными.
Изображение на эпюре Монжа параллельных прямых, прямой и плоскости, плоскостей базируется на инвариантном свойстве 2з (см. § 6) ортогонального проецирования.
1. Параллельные прямые.
Если а || b, то а ∩ b в несобственной точке К∞, следовательно, ее проекции К'∞ и К"∞ будут также несобственными. Поэтому а' || b' и а" || b", т. е. у параллельных прямых параллельны их одноименные проекции.
2. Параллельность прямой и плоскости.
Если а ∩ α = K∞ - несобственная точка (иначе а || α), то ее проекции будут также несобственными точками K'∞ и К"∞. Поэтому а' || α' и а" || α".
Известно, что прямая, параллельная плоскости, должна быть параллельна какой-либо прямой, принадлежащей этой плоскости. Поэтому, чтобы задать на эпюре Монжа прямую а, параллельную плоскости α, необходимо и достаточно в плоскости α "взять" произвольную прямую b и провести а || b по правилу, изложенному в п. 1.
3. Параллельные плоскости.
Две плоскости параллельны, если в одной из них можно провести две пересекеющиеся прямые, параллельные двум пересекающимся прямым другой плоскости. Поэтому, чтобы задать на эпюре Монжа плоскость α(a ∩ b), параллельную плоскости β(m ∩ n), достаточно указать проекции пересекающихся прямых а и b, соответственно параллельных прямых m и n.
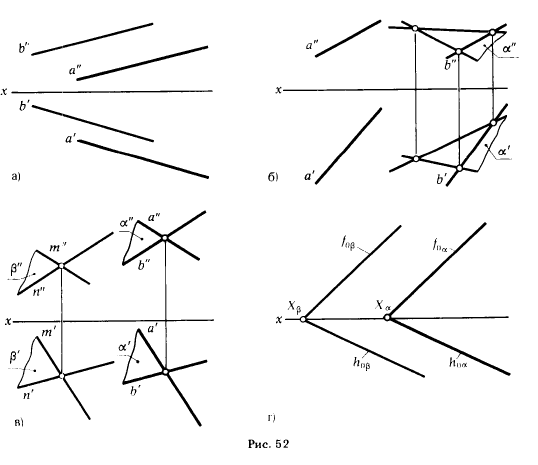
В частности, если плоскости заданы следами, то у параллельных плоскостей будут параллельны их одноименные следы. На рис. 52 показаны эпюры: параллельных прямых а || b (рис. 52,а); параллельных прямой а и плоскости α (рис. 52,6); параллельных плоскостей α и β (рис. 52,в и г). На рис. 52,в плоскость α (a ∩ b), плоскость β(m ∩ n), на рис. 52,г плоскости заданы следами.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- В чем состоит реконструкция трехмерного евклидова пространства?
- Что такое несобственные элементы пространства?
- Сформулируйте основные отношения принадлежности между элементами евклидова пространства.
- Перечислите основные способы метода проекции.
- Какие преимущества присущи ортогональному проецированию по сравнению с косоугольным проецированием?
- Укажите основные инвариантные свойства ортогонального проецирования.
- Каким образом пространственная фигура из трех взаимно перпендикулярных плоскостей преобразуется в плоскую модель?
- Какой октант имеет отрицательное направление всех осей?
- Какими полами плоскостей проекций ограничены II, III, VI, VII октанты?
- Как обозначаются проекции точки, прямой, плоскости на плоскостях проекций?
- Как по отношению к осям проекций располагаются проекции точек, находящихся в I, II, III, ... , VIII октантах?
- Какие знаки имеют координаты х, у, z точки, находящейся в I, II, III, ... ... , VIII октанте?
- Какие координаты на эпюре определяют горизонтальную и фронтальную проекции точки?
- В каких октантах значения координат точки отрицательны, в каких положительны?
- Как определить положение третьей проекции точки на безосном чертеже, если известны две ее проекции и три проекции другой точки?
- Дайте определение и способы нахождения следов прямой и плоскости.
- Какие линии плоскости называются главными, перечислите характерные особенности проекций этих линий на эпюре Монжа.
- Какие прямые и плоскости называются проецирующими, в чем состоит отличительная особенность их ортогональных проекций?