Реконструкция евклидова пространства
ТеорияПринятие аксиомы Евклида о параллельности при последующем изложении приводит к определенным трудностям, вызванным тем, что, рассматривая метод проекций, составляющий основу для изображения на плоскости геометрических фигур, расположенных в пространстве, мы обнаруживаем "неоднородность" евклидова пространства и погруженных в него геометрических фигур.
Действительно, пусть даны две прямые а и b, определяющие плоскость α (рис. 1). Возьмем в плоскости α произвольную точку S (S∉а∧b). Через точку S проведем произвольную прямую l, которая пересечет прямую а в точке Аа, а прямую b в точке Аb. Проведем через точку S прямую l1 , пересекающую прямую а в точке Ва, а прямую b в точке Вb. Аналогично, прямые l2, l3, проведенные через точку S, пересекают прямые а и b соответственно в точках Сa и Сb, Da и Db.
Выполненные построения показывают, что мы каждый раз получаем две точки - одну на прямой а и одну, однозначно соответствующую ей точку, на прямой b. Так будет продолжаться до тех пор, пока в пучке
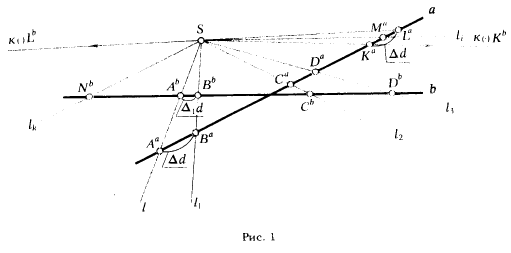
прямых с центром в точке S не появится прямая li, параллельная прямой b. Эта прямая пересекает прямую а в точке Ма. Ввиду параллельности прямых li и b они не будут пересекаться, следовательно, не будет и точки Мb на прямой b, однозначно соответствующей точке Мa, т. е. выявленная ранее закономерность, состоящая в том, что каждой точке прямой а соответствует точка прямой b и наоборот, нарушается с появлением параллельной прямой. Кроме точки Мa появится еще одна точка Nb(Nb∈b), которая также будет отличаться от всех остальных точек прямой b (так как lk||а). Рис. 1 показывает, что мы оказываемся перед фактом, что прямые а и b (из-за аксиомы о параллельности) не являются однородными: каждая из них содержит точку (Мa и Nb соответственно), отличную от всех других точек, объединенных в прямые а и b.
Свойства евклидовой плоскости обнаруживают еще одно несоответствие, которое влечет за собой нарушение принципа взаимной непрерывности.
Действительно, если расстояние Δd между точками Аa и Ва прямой а - величина бесконечно малая (см. рис. 1), то и расстояние Δ1d между соответствующими этим точкам точками Аb и Вb прямой b будет также бесконечно малым.
Приведенные рассуждения будут справедливы и для другой пары соответственных точек (например, CаDа и CbDb).
Но если мы возьмем на прямой а две бесконечно близкие точки Ка и Lа, разделенные точкой Ма, то, как видно из чертежа, им будут соответствовать две бесконечно удаленные точки Кb и Lb прямой b.
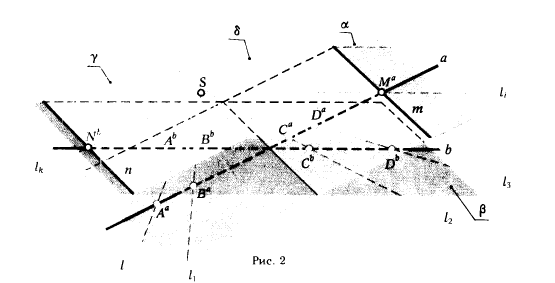
Если мы обратимся к трехмерному евклидову пространству, то в нем появится множество точек, принадлежащих прямым m и п, по которым пересекаются плоскости α и β с плоскостями δ и γ, определяемыми пучками прямых, параллельных плоскостям α и β и принадлежащих точке S (рис. 2).
Становится очевидным, что евклидово пространство, свойства которого определяются, в частности, и аксиомой о параллельности, не может быть использовано для разработки метода центрального проецирования. Более того, мы оказываемся перед альтернативой: или принять на веру существование аксиомы о параллельности и, как следствие, признать неоднородность окружающего нас пространства, или считать, что пространство однородно, подвергнув сомнению существование аксиомы о параллельности.
Для того чтобы освободиться от указанных недостатков, необходимо трехмерное евклидово пространство подвергнуть реконструкции.
Из рис. 1 видно, что для того чтобы точка Ма не отличалась от остальных точек (Аа, Ва, Са, Dа) прямой а, достаточно потребовать, чтобы параллельные прямые li, и b пересекались; при этом точку их пересечения Мb будем считать бесконечно удаленной - несобственной точкой (в отличие от точек евклидова пространства, которые считаются собственными).
Таким образом, дополнение прямой несобственной точкой, в которой прямая пересекается с параллельной прямой, позволяет устранить недостаток, являющийся следствием аксиомы о параллельности.
Теперь мы можем утверждать, что любая точка прямой а будет иметь соответствующую ей точку на прямой b. Эта точка может быть как собственной, так и несобственной.
Наличие на прямой несобственной точки позволяет установить не только взаимно-однозначное соответствие между точками прямых а и b, но и ликвидирует и второе несоответствие, связанное с нарушением непрерывности в расположении точек, принадлежащих прямой. Точки Кb и Lb прямой b, соответствующие бесконечно близким точкам Ка и Lа прямой а, удалены в бесконечность, и расстояние между ними бесконечно большое.
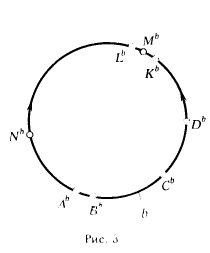
В то же время расстояние между точками КаМа и LаMа прямой а бесконечно мало. Для того чтобы избежать разрыва прямой b, достаточно предположить, что расстояние между точками КbМb и LbMb так же бесконечно мало, как и между двумя другими бесконечно близкими точками KbLb. Это может произойти лишь в том случае, если прямая b будет замкнутой. Условная модель такой прямой показана на рис. 3.
На плоскости можно провести бесчисленное множество прямых, каждая из которых имеет несобственную точку. Что же представляет из себя множество этих точек плоскости?
Так как каждая прямая плоскости имеет только одну несобственную точку, то она может пересекать множество этих несобственных точек только в одной точке, поэтому естественно считать множество несобственных точек плоскости несобственной прямой. Выясним также, что представляет собой множество несобственных точек пространства.
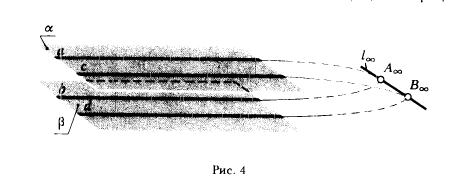
Представим две параллельные плоскости α и β (рис. 4). Проведем в каждой из них по одной прямой а и b так, чтобы а || b. Эти прямые пересекутся в несобственной точке А∞, . Проведем в плоскости α прямую с, а в плоскости β прямую d, причем с || d. Эти прямые пересекутся также в несобственной точке В∞. Несобственные точки A∞ и В∞ определяют несобственную прямую l∞. Так как точки А∞ и В∞ принадлежат как плоскости α, так и плоскости β, то несобственная прямая также принадлежит этим плоскостям. Следовательно, в евклидовом пространстве, дополненном несобственными точками, две параллельные плоскости пересекаются по бесконечно удаленной - несобственной прямой. Ранее было установлено, что множество несобственных точек пространства пересекаются прямой в одной несобственной точке. Теперь мы показали, что это же множество имеет с плоскостью одну общую несобственную прямую.
Естественно считать множество несобственных точек пространства несобственной (бесконечно удаленной) плоскостью *.
Итак, для реконструкции евклидова пространства достаточно: дополнить множество точек прямой несобственной точкой, что приводит к дополнению евклидовой плоскости несобственной прямой, а трехмерное пространство - несобственной плоскостью.
Дополненные несобственными элементами евклидовы плоскость и пространство называют соответственно проективной плоскостью и проективным пространством.
Отмеченные ранее в пп. 5, 6, 7 (см. § 1, с. 14) свойства евклидова пространства для проективного пространства могут быть сформулированы иначе:
п. 5 - две прямые, принадлежащие одной плоскости, всегда принадлежат одной и той же и только одной точке;
п. 6 - две различные плоскости всегда принадлежат одной и той же и только одной прямой;
п. 7 - плоскость и не принадлежащая ей прямая всегда принадлежат одной и той же и только одной точке.
Во всех рассмотренных случаях точка и прямая могут быть как собственными, так и несобственными.