Прямая и точка в плоскости. Прямые особого положения

Как построить на чертеже прямую линию, лежащую в заданной плоскости? Это построение основано на двух положениях, известных из геометрии.

1. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
2. Прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельной ей.

Положим, что пл.α (рис. 106) определена двумя пересекающимися прямыми АВ и СВ, а пл. β — двумя параллельными — DE и FG. Согласно первому положе

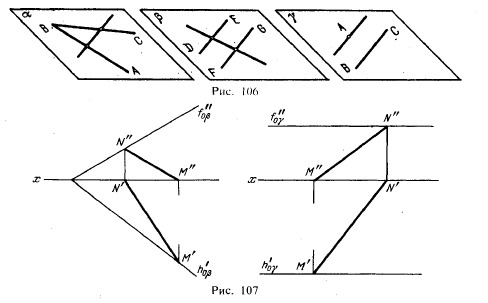
нию прямая, пересекающая прямые, определяющие плоскость, находится в данной плоскости.

Отсюда вытекает, что если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости (рис. 107).

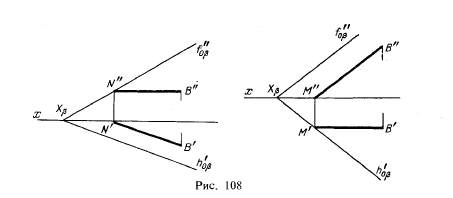
Положим, что пл. γ (рис. 106) определяется точкой А и прямой ВС. Согласно второму положению прямая, проведенная через точку А параллельно прямой ВС, принадлежит пл. γ. Отсюда прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 108).

Примеры построений на рис. 107 и 108 не должны быть поняты так, что для построения прямой в плоскости надо предварительно строить следы этой плоскости. Это не требуется.

Например, на рис. 109 выполнено построение прямой AM в плоскости, заданной точкой А и прямой, проходящей через точку L. Положим, что прямая AM должна быть параллельна пл. π₁. Построение начато с проведения проекции А"М" перпендикулярно к линии связи А"А'. По точке М" найдена точка М', и затем проведена проекция А'М'. Прямая AM отвечает условию: она параллельна пл. π₁ И лежит в данной плоскости, так как проходит через две точки (А и М), заведомо принадлежащие этой плоскости.

Как построить на чертеже точку, лежащую в заданной плоскости? Для того чтобы сделать это, предварительно строят прямую, лежащую в заданной плоскости, и на этой прямой берут точку.

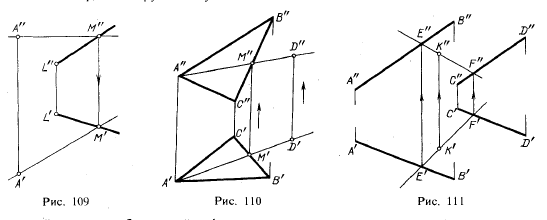
Например, требуется найти фронтальную проекцию точки D, если задана ее горизонтальная проекция D' и известно, что точка D должна лежать в плоскости, определяемой треугольником АВС (рис. 110).

Сначала строят горизонтальную проекцию некоторой прямой так, чтобы точка D могла оказаться на этой прямой, а последняя была бы расположена в данной плоскости. Для этого проводят прямую через точки А' и D' и отмечают точку М', в которой прямая A'D' пересекает отрезок В'С'. Построив фронтальную проекцию М" на В"С", получают прямую AM, расположенную в данной плоскости: эта прямая проходит через точки А и М, из которых первая заведомо принадлежит данной плоскости, а вторая в ней построена.

Искомая фронтальная проекция D" точки D должна быть на фронтальной проекции прямой AM.

Другой пример дан на рис. 111. В пл. β, заданной параллельными прямыми АВ и CD, должна находиться точка К, для которой дана лишь горизонтальная проекция — точка К

Через точку К' проведена некоторая прямая, принимаемая в качестве горизонтальной проекции прямой в данной плоскости. По точкам E' и F' строим Е" на А"В" и F" на C"D". Построенная прямая EF принадлежит пл. β, так как проходит через точки Е и F, заведомо принадлежащие плоскости. Если взять точку К" на E"F", го точка К окажется в пл.β

К числу прямых, занимающих особое положение в плоскости, отнесем горизонтали, фронтали ¹) и линии наибольшего наклона к плоскостям проекций. Линию наибольшего наклона к пл. π₁, будем называть линией ската плоскости ²).

Горизонталями плоскости называются прямые, лежащие в пей и параллельные горизонтальной плоскости проекций.

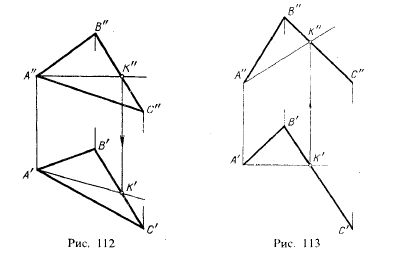
Построим горизонталь плоскости, заданной треугольником АВС. Требуется провести горизонталь через вершину А (рис. 112).

Так как горизонталь плоскости есть прямая, параллельная пл.π₁, то фронтальную проекцию этой прямой получим, проведя А"К"⊥А"А'. Для построения горизонтальной проекции этой горизонтали строим точку К' и проводим прямую через точки А' и К'.

Построенная прямая АК действительно является горизонталью данной плоскости: эта прямая лежит в плоскости, так как проходит через две точки, заведомо ей принадлежащие, и параллельна плоскости проекций π₁.

Теперь рассмотрим построение горизонтали плоскости, заданной следами.

Горизонтальный след плоскости есть одна из ее горизонталей («нулевая» горизонталь). Поэтому построение какой-либо из горизонталей плоскости сводится

к проведению в этой плоскости прямой, параллельной горизонтальному следу плоскости (рис. 108, слева). Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости; фронтальная проекция горизонтали параллельна оси проекций.

Фронталями плоскости называются прямые, лежащие в ней и параллельные плоскости проекций π₂.

Пример построения фронтали в плоскости дан на рис. 113. Пост роение выполнено аналогично построению горизонтали (см. рис. 112).

Пусть фронталь проходит через точку А (рис. 113). Начинаем построение с проведения горизонтальной проекции фронтали — прямой А'К', так как направление этой проекции известно: А К'⊥А"А'. Затем строим фронтальную проекцию фронтали — прямую А"К".

¹)Наряду с горизонталями и фронталями плоскости можно рассматривать также ее профильные прямые — прямые, лежащие в данной плоскости и параллельные пл. π₃. Для горизонталей, фронталей и профильных прямых встречается общее название — линия уровня. Однако такое название отвечает обычному представлению только о горизонтальности.

²)Для линии ската плоскости распространено название «линия наибольшего ската», но понятие «скат» по отношению к плоскости не требует добавления «наибольший».

Построенная прямая действительно является фронталью данной плоскости: эта прямая лежит в плоскости, так как проходит через две точки, заведомо ей принадлежащие, и параллельна пл, π₂.

Построим теперь фронталь плоскости, заданной следами. Рассматривая рис, 108, справа, на котором изображена пл. β и прямая МВ, устанавливаем, что эта прямая — фронталь плоскости. Действительно, она параллельна фронтальному следу («нулевой» фронтали) плоскости, Горизонтальная проекция фронтали параллельна оси х, фронтальная проекция фронтали параллельна фронтальному следу плоскости.

Линиями наибольшего наклона плоскости к плоскостям π₁, π₂ и π₃ называются прямые, лежащие в ней и перпендикулярные или к горизонталям плоскости, или к ее фронталям, или к ее профильным прямым. В первом случае определяется наклон к пл.π₁, во втором — к пл. π₂, в третьем — к пл. π₃. Для проведения линий наибольшего наклона плоскости можно, конечно, соответственно брать ее следы.

Как было сказано выше, линия наибольшего наклона плоскости к пл. к π₁, называется линией ската плоскости.

Согласно правилам проецирования прямого угла (см, § 15) горизонтальная проекция линии ската плоскости перпендикулярна к горизонтальной проекции горизонтали этой плоскости или к ее горизонтальному следу. Фронтальная проекция линии ската строится после горизонтальной и может занимать различные положения в зависимости от задания плоскости. На рис, 114 изображена линия ската Пл. α: ВК⊥h'_0α. Так как В'К также перпендикулярна к h'_0α, то ∠ВКВ' есть линейный угол

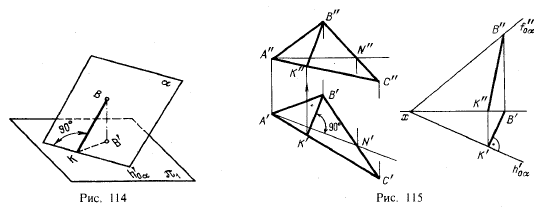
двугранного, образованного плоскостями α и π₁ Следовательно, линия ската плоскости может служить для определения угла наклона этой плоскости к плоскости проекций π₁.

Аналогично, линия наибольшего наклона плоскости к пл, π₂ служит для определения угла между этой плоскостью и пл, π₂, а линия наибольшего наклона к пл.π₃ — для определения угла.с пл. π₃.

На рис, 115 построены линии ската в заданных плоскостях. Угол пл, α с пл.π₁ выражен проекциями — фронтальной в виде угла В"К"В' и горизонтальной в виде отрезка К'В'. Определить величину этого угла можно, построив прямоугольный треугольник по катетам, равным К'В' и В"В'.

Очевидно, линия наибольшего наклона плоскости определяет положение этой плоскости. Например, если (рис. 115) задана линия ската КВ, то, проведя перпендикулярную к ней горизонтальную прямую AN или задавшись осью проекций х и проведя h'_0α⊥ К'В', мы вполне определяем плоскость, для которой КВ является линией ската.

Рассмотренные нами прямые особого положения в плоскости, главным образоии горизонтали и фронтали, весьма часто применяются в различных построениях и при решении задач. Это объясняется значительной простотой построения указанных прямых; их поэтому удобно применять в качестве вспомогательных.

На рис. 116 была задана горизонтальная проекция К' точки К. Требовалось найти фронтальную проекцию К", если точка К должна быть в плоскости, заданной двумя параллельными прямыми, проведенными из точек А и В.

Сначала была проведена некоторая прямая линия, проходящая через точку К и лежащая в заданной плоскости. В качестве такой прямой выбрана фронталь МN: ее горизонтальная проекция проведена через данную проекцию К'. Затем построены точки М" и N", определяющие фронтальную проекцию фронтали.

Искомая проекция К" должна находиться на прямой M"N".

На рис. 117 слева по данной фронтальной проекции А" точки А, принадлежащей пл.α, найдена ее горизонтальная проекция (А'); построение произведено при помощи горизонтали ЕК. На рис. 117 справа аналогичная задача решена при помощи фронтали MN.

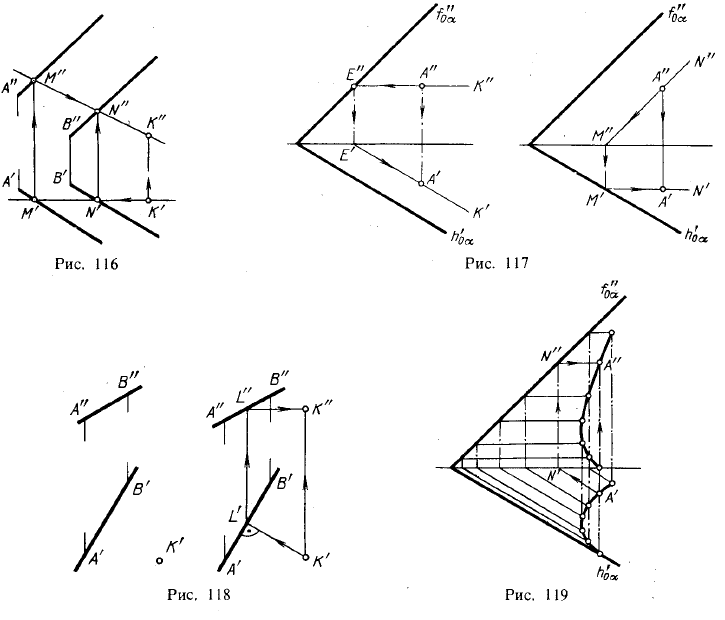
Еще один пример построения недостающей проекции точки, принадлежащей некоторой плоскости, дан на рис. 118. Слева показано задание: линия ската плоскости (АВ) и горизонтальная проекция точки (К'). Справа на рис. 118 показано построение; через точку К' проведена (перпендикулярная к А'В') горизонтальная проекция горизонтали, на которой должна лежать точка К, по точке L" найдена фронтальная проекция этой горизонтали и на ней искомая проекция К".

На рис. 119 дан пример построения второй проекции некоторой плоской кривой, если известна одна проекция (горизонтальная) и пл. α, в которой эта кривая расположена. Взяв на горизонтальной проекции кривой ряд точек, находим при помощи горизонталей точки для построения фронтальной проекции кривой.

Стрелками показан ход построения фронтальной проекции А" по горизонтальной проекции А'.

Вопросы к §§ 16-18

1. Как задаетcя плоскость на чертеже?
2. Что такое след плоскости на плоскости проекций?
3. Где располагаются фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа плоскости?
4. Как определяется на чертеже, принадлежит ли прямая данной плоскости?
5. Как построить на чертеже точку, принадлежащую данной плоскости?
6. Что такое фронталь, горизонталь и линия ската плоскости?
7. Может ли служить линия ската плоскости для определения угла наклона этой плоскости к плоскости проекций π₁?
8. Определяет ли прямая линия плоскость, для которой эта прямая является, линией ската?