Решение позиционных задач на аксонометрических проекциях

Решение позиционных задач на аксонометрическом чертеже не отличается от решения этих задач в ортогональных проекциях на эпюре Монжа.

Алгоритмы решения задач для определения линии пересечения двух поверхностей (см. § 43, табл. 8) и нахождения точек встречи линии С поверхностью (см. § 53, табл. 9), составленные для ортогональных проекций, остаются без изменения при решении аналогичных задач в аксонометрических проекциях. Рассмотрим решение основных позиционных задач: определение точки встречи прямой с плоскостью и построение линии пересечения двух поверхностей.

ЗАДАЧА 1. Определить точку К = m ∩ β (рис. 317).

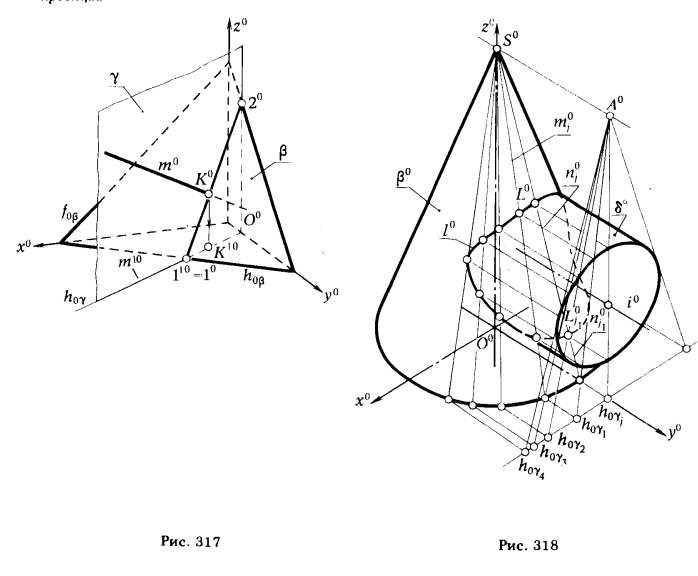
РЕШЕНИЕ.

1. Заключаем данную прямую m во вспомогательную плоскость γ, перпендикулярную какой-либо координатной плоскости (на рис. 317 γ ⊥ плоскости O⁰x⁰у⁰). Горизонтальный след h_0γ плоскости у совпадает со вторичной проекцией m^{1 0} прямой m.

2. Отмечаем (1⁰2⁰), по которой пересекаются плоскости γ и β: (1⁰2⁰) = γ ∩ β.

3. Находим К⁰ = m⁰ ∩ (1⁰2⁰).

4. Зная К⁰ , определяем вторичную проекцию К^{1 0} .

ЗАДАЧА 2. Построить линию l⁰ пересечения конической β и цилиндрической δ поверхностей l⁰ = β ∩ δ (рис. 318).Эта задача может быть решена двумя способами.

Способ 1. Решают эту задачу в ортогональных проекциях, а затем строят аксонометрическую проекцию полученной линии пересечения.

Способ 2. Состоит в построении искомой линии пересечения непосредственно на аксонометрической проекции. При этом решение осуществляется по алгоритму, составленному для решения аналогичной задачи в ортогональных проекциях.

Решение приведено на рис. 318. Как видно из чертежа, для определения точек (L⁰_j и L⁰_j1) ∈ l⁰_j (L⁰_j = m⁰_j ∩ n⁰_j) используются плоскости, принадлежащие пучку плоскостей, проходящих через прямую SA. Любая плоскость этого пучка пересекает поверхности β и δ по прямым m⁰ и n⁰.

Точки L⁰_j и L⁰_j1 принадлежат искомой линии пересечения поверхностей β и δ.