О родственном соответствии и его применении к решению некоторых задач
ТеорияРассмотрим родственное соответствие фигур, расположенных в двух пересекающихся плоскостях или в одной плоскости, в системе параллельного проецирования.
На рис. 484 точки А1 и В1 плоскости β параллельно спроецированы по направлению, заданному стрелкой, на пл. α. Проецирующие прямые А1А2 и В1В2 определяют проецирующую плоскость, которая пересекает плоскости β и α по прямым СВ1 и СВ2, сходящимся на прямой MN в точке С.
Если взять в пл. β некоторую прямую А1В1 то проекция этой прямой на пл. α при своем продолжении встретит на линии пересечения плоскостей β и α саму прямую А1В1.
Параллельное проецирование точек пл. β на пл. α устанавливает между этими плоскостями некоторое соответствие: точке А1 в пл. β соответствует точка 2 в пл. α, тоцке В1 — точка В2 и т. д. Это соответствие обладает следующими основными свойствами:
- каждой точке одной плоскости соответствует единственная точка другой плоскости (соответствие взаимно однозначное);
- если на прямой, расположенной в одной плоскости, установлено наличие двух точек, соответствующих точкам прямой другой плоскости, то эти прямые соответствуют одна другой, причем каждой точке одной из этих прямых соответствует определенная точка другой прямой;
- прямая одной плоскости пересекается с соответствующей ей прямой другой плоскости в точке, лежащей на линии пересечения плоскостей 1);
- прямая, по которой пересекаются обе плоскости, сама себе соответствует;
- если прямые одной плоскости параллельны между собой, то и соответствующие им прямые другой плоскости параллельны между собой;
- отношение двух отрезков в одной плоскости, лежащих на одной прямой или на параллельных прямых, равно отношению соответствующих отрезков в другой плоскости.
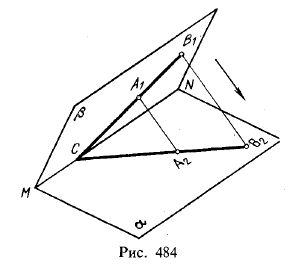
Рассмотренное соответствие между двумя плоскостями, обладающее перечисленными свойствами, называется родственным соответствием или, короче, родством 2). На рис. 484 точки А2 и В2 родственны точкам А1 и В1; прямая А2В2 родственна прямой А1В1.
Если в пл. β взять какую-нибудь фигуру и в пл. α рассмотреть точки, родственные всем точкам этой фигуры, то совокупность последних дает на пл. α фигуру, родственную фигуре, взятой на пл. β.
1) Если эти прямые параллельны линии пересечения плоскостей, то точка пересечения прямых является бесконечно удаленной.
2) Родственное соответствие является частным случаем аффинного соответствия двух плоскостей, изучаемого в высшей геометрии. Affinis (лат.) — смежный, соседний; affinitas — родство, свойство.
Прямая MN пересечения плоскостей называется осью родства.
На рис. 485 слева те же плоскости даны в совмещенном положении: пл. β вращением вокруг прямой MN совмещена с пл. α.
Если взять обратное направление вращения, то получим расположение совмещенных плоскостей, показанное на рис. 485 справа.
Если между плоскостями β и α в пространстве было установлено родственное соответствие, то и после совмещения этих плоскостей (рис. 485) между их точками, прямыми и фигурами будет также иметь место родственное соответствие, по своим свойствам совпадающее со свойствами родства, установленного при параллельном проецировании. Действительно,
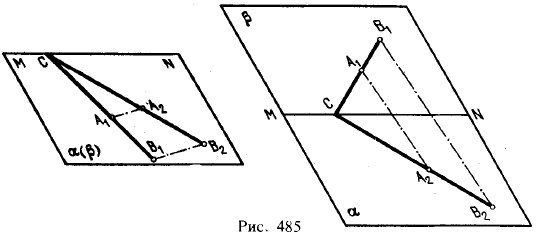
в обоих случаях прямой линии соответствует прямая, точке на одной из прямых соответствует определенная точка на другой, отношение CA1/A1B1 остается равным отношению CA2/A2B2 и параллельность проецирующих прямых А1А2 и В1В2 (рис. 484) переходит в параллельность прямых A1A2 и B1B2 на рис. 485 при совмещении плоскостей.
Итак, вне зависимости от того, рассматриваем ли мы родственные прямые в пространстве или при совмещении плоскостей, родственные прямые пересекаются на оси родства и точки, соответствующие друг другу, лежат на прямых, параллельных между собой.
Направление прямой A1A2 теперь уже не является направлением проецирования (как на рис. 484); будем называть его направлением родства.
Если на чертеже двух совмещенных плоскостей даны ось родства и две точки, родственные друг другу, то для каждой другой точки в данном родстве может быть найдена родственная точка. Положим (рис. 486), что прямая MN есть ось родства, точки A1 и A2 — родственные точки и, следовательно, A1A2 есть направление родства. Требуется для точки B2 найти родственную точку. Проводим прямую В2A2 до пересечения с MN; через точки
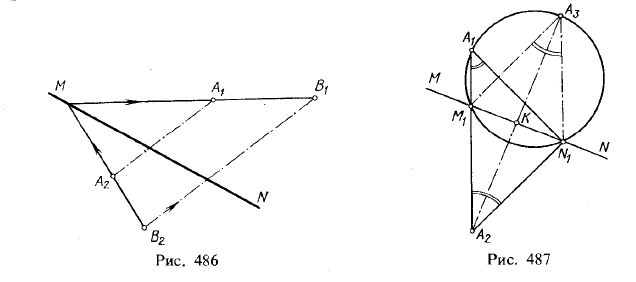
С и A1 (см. рис. 485) проводим прямую, на которой и находим точку В1 родственную точке В2 , проводя прямую В2В1 параллельно А2 А1 . Умея строить родственные точки, можно построить фигуру, родственную любой заданной фигуре.
Если заданная фигура — многоугольник, то родственная ей фигура тоже многоугольник с тем же числом сторон, и для его построения достаточно найти точки, родственные вершинам, и соединить их прямолинейными отрезками. Если же заданная фигура криволинейная, то построение родственной ей фигуры производится по нескольким ее точкам; через полученные точки проводится кривая.
Рассматривая фигуру, родственную заданной фигуре, мы замечаем, что величина углов вообще не сохраняется (см., например, рис. 491: углы четырехугольника A'B'C'D' не равны соответствующим им углам в родственном четырехугольнике АBCD).
Однако при заданной оси родства MN (рис. 487), паре родственных точек А1 и А2 и паре родственных прямых А1М1и А2М1. проходящих через эти точки, можно построить еще одну пару родственных прямых A1N1 и А2N1 , так, что угол M1A1N1 будет равен углу М1A2N1 . Из точки А2 проведен перпендикуляр к прямой MN и построена точка А3 так, что А2К = КА3, Через точки А1, А3 и М1 проведена окружность, которая пересекает прямую MN еще в точке N1. Дальнейшее ясно из чертежа.
В родственном соответствии двух плоскостей, заданных осью и двумя родственными точками А1 и А2, можно построить два взаимно перпендикулярных направления одной из плоскостей, соответствующих двум взаимно перпендикулярным направлениям другой плоскости. Такие направления называются главными в данном родственном соответствии. Построение показано на рис. 488. Отрезок прямой А1А2 разделен пополам в точке К, и через
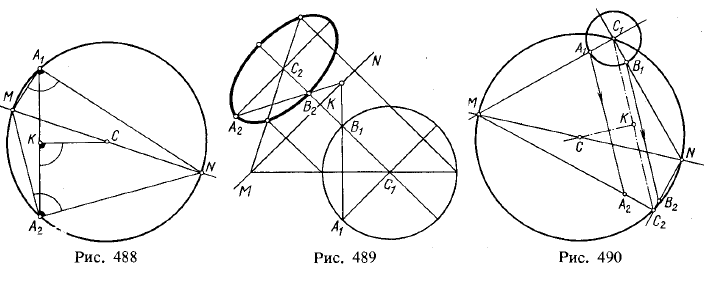
эту точку проведен перпендикуляр к А1А2 до пересечения с MN в точке С. Из точки С проведена окружность через точки A1 и А2. Получены две пары родственных прямых: А1М и А2М, A1N и A2N. Углы MA1N и MA2N прямые.
Фигура, родственная окружности, будет вообще эллипсом, причем взаимно перпендикулярные диаметры окружности переходят в сопряженные диаметры эллипса.
На рис. 489 изображены ось родства MN и две родственные точки С1 и С2, причем точка C1 является центром заданной окружности. Направление родства С1С2 расположено перпендикулярно к оси. Построена фигура, родственная окружности,— эллипс с центром С2. Полуоси эллипса А2С2 и В2С2 получены как прямые, родственные двум взаимно перпендикулярным радиусам A1C1 и В1С1. В данном случае прямой угол А2С2К, родственный прямому углу А1С1К, получен проведением прямой А2С2||MN, так как С1A1||MN.
На рис. 490 показано построение полуосей А2С2 и В2С2 эллипса, родственного окружности с центром С1, когда направление родства С1С2 не перпендикулярно к оси родства. Применено вспомогательное построение по рис. 488 для нахождения главных направлений МС1 и NC1, МС2 и NС2, которые определяют направления тех взаимно перпендикулярных диаметров окружности, которые преобразуются в оси эллипса (на рис. 490 показано построение только полуосей А2С2 и В2С2).
Если взять некоторую плоскость общего положения в системе плоскостей π1, π2 и π3, то между плоскостью α и каждой из плоскостей проекций имеет место упомянутое выше родственное соответствие, так как ортогональное проецирование есть частный случай общего параллельного проецирования. Следы плоскости а будут осями родства; след h'0α — для плоско
стей α и π1, след f"0α — для α и π2; след p'"0α — для α и π3. Прямая, расположенная в пл. α, и каждая из ее проекций пересекаются на соответствующих следах плоскости, т. е. на осях родства.
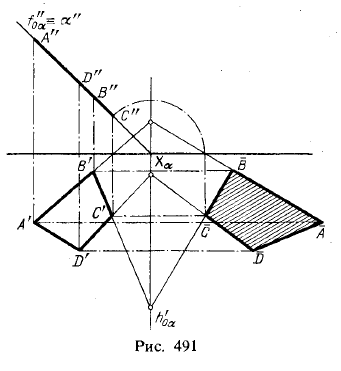
На рис. 491 выполнено построение четырехугольника АBCD(натурального его вида) как фигуры, родственной проекции А'В'С'D'. След h'0α фронтально-проецирующей плоскости, в которой находится данный четырехугольник, служит осью родства; направление родства перпендикулярно к h'0α. Находим обычным путем (способ совмещения) точку C, родственную точке С', а затем строим точки АBDпо схеме, указанной на рис. 486.
Рис. 492 показывает, что между горизонтальной и фронтальной проекциями всякой плоской фигуры (в данном случае треугольника) существует родственное соответствие.
Прежде всего отмечаем, что прямые, соединяющие точки А' и А", В' и В", С' и С", параллельны между собой. Далее следует установить, что любые две прямые, соответствующие одна другой, пересекаются на одной и той же прямой. Продолжим до пересечения прямые А'В' и А"В". Точка М2 представляет собой одновременно горизонтальную и фронтальную проекции точки, принадлежащей прямой АВ в пространстве. Совпадение проекций показывает, что эта точка находится на равных расстояниях от плоскостей π1 и π2.
То же можно сказать и относительно точек М1 и М3. Равноудаленность точек от плоскостей π1 и π2позволяет заключить, что точки эти, принадлежа плоскости треугольника АВС, находятся в то же время в плоскости, делящей второй и четвертый углы (четверти) пространства пополам.
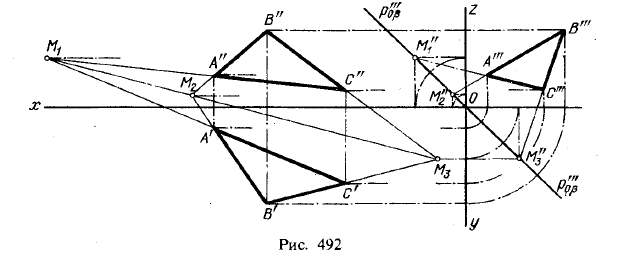
На рис. 492 эта плоскость выражена следом p"'0β - Так как рассматриваемые точки одновременно должны принадлежать двум плоскостям — пл. β и плоскости треугольника АВС, то очевидно, что они должны лежать на линии пересечения плоскости треугольника АВС и пл. β. Прямая эта, находясь в плоскости, делящей второй и четвертый углы (четверти) пространства пополам, изобразится на плоскостях π1 и π2 одной и той же прямой (горизонтальная и фронтальная проекции совпадают), а следовательно, точки М1 , М2 и М3 расположены на одной прямой, которая и служит осью родства. Проекции любой прямой, лежащей в плоскости треугольника АВС, пересекаются на найденной оси родства 1).
1) Если прямая расположена в плоскости треугольника АВС и параллельна оси родства, то она пересекается с осью родства в бесконечности; обе ее проекции параллельны оси родства.
Итак, проекции А'В'С и А"В"С" родственны; направление родства перпендикулярно к оси х, ось родства располагается вообще под некоторым углом к оси х. В случае, если плоскость данной фигуры проходит через ось х, то ось родства горизонтальной и фронтальной проекций совпадает с осью х.
Для горизонтальных и фронтальных проекций всех фигур, расположенных в одной и той же плоскости, получается общая ось родства; действительно, эта ось представляет собой совпавшие горизонтальную и фронтальную проекции линии пересечения некоторой плоскости с постоянной плоскостью β (рис. 492).
На рис. 493 родственное соответствие применено для построения горизонтальной проекции четырехугольника, если известна его фронтальная проекция A"B"C"D" й горизонтальные проекции трех вершин (точки А', В', С).
Прежде всего найдены точки М1 и М2 и тем самым определена ось родства. Затем прямая A"D" продолжена до пересечения с осью родства и полученная точка М3 соединена прямой с точкой А'.
Искомая точка D' получится в пересечении прямой А'М3 и линии связи D”D'. Остается соединить между собой прямыми точки А' и D', точки С' и D'.
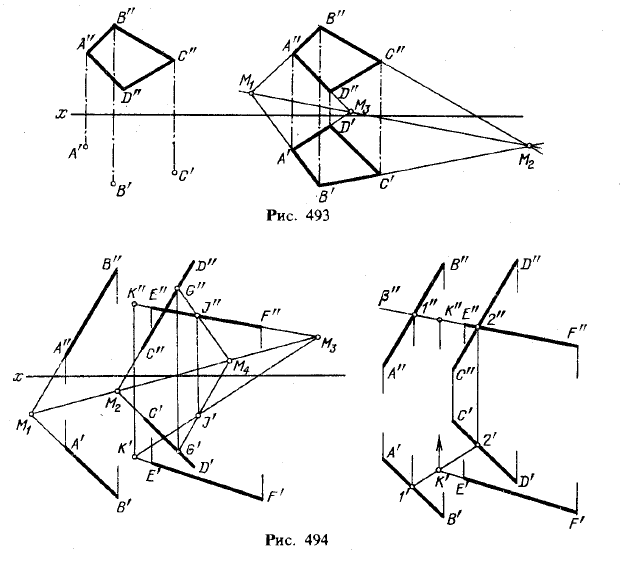
На рис. 494 слева родственное соответствие применено для отыскания проекций точки пересечения прямой EF с плоскостью, заданной двумя параллельными прямыми АВ и CD.
Задача сводится к отысканию на прямых E'F' и E"F" точек, являющихся родственными друг другу в данном родственном соответствии. Это соответствие определяется любыми двумя родственными точками (на рис. 494 взяты точки G' и G") и осью родства, проведенной через точки М1 и М2, которые найдены в пересечении прямых А'В' и А”В", C'D' и C"D". Если, далее, построить прямую, родственную прямой E”F", то мы тем самым в плоскости, заданной прямыми АВ и CD, проведем некоторую новую прямую, находящуюся в то же время в одной плоскости с данной прямой EF (общая фронтальная проекция E"F").
Построение прямой, родственной прямой E"F" выполнено следующим образом: пользуясь родственными точками G' и G" и произвольно выбранной точкой I" на прямой E"F",
строим точку I', родственную точке I" если, далее, найти точку М3 и провести через нее и через точку I' прямую, то определится прямая, родственная прямой E"F". Остается отметить точку K', в которой прямые I'3 и E'F' пересекают друг друга, Эта точка К' является горизонтальной проекцией искомой точки пересечения.
На рис. 494 справа показано решение той же задачи, но приемом, изложенным в § 25; через прямую EF проведена плоскость β, построена прямая с проекциями 1"2" и 1'2', по которой пл. β пересекает заданную плоскость, получена проекция К' искомой точки, а по ней — проекция К". Это построение проще показанного на рисунке слева.
Но в примере, приведенном на рис. 495, применение родственного соответствия позволяет построить оси эллипса (что не было сделано на рис. 364 — 366 в § 56), не прибегая к переходу от его сопряженных диаметров к осям.
Не объясняя нахождения ряда точек эллипса — фронтальной проекции сечения цилиндра плоскостью (это было сделано в § 56), остановимся здесь лишь на построении осей эллипса.
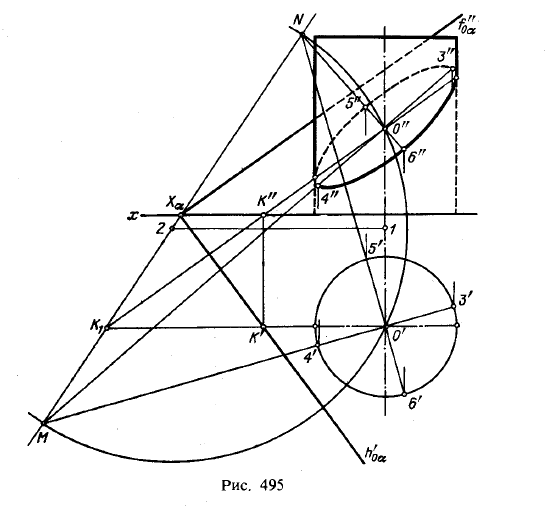
Проекции фигуры сечения — эллипс и окружность — родственны при направлении родства, перпендикулярном к оси х. Ось родства — прямая MN — строится при помощи родственных между собою в том же родстве проекций К"О” и К'О', а также хотя бы следа f"0α и оси х: найдя точку К1 и проведя через нее и через Хα прямую, получаем ось родства. Теперь приемом, показанным на рис. 490, находим взаимно перпендикулярные направления — для фронтальной проекции NO" и МO” и для горизонтальной проекции NО' и МО', а по точкам 3' и 4' — вершины эллипса 3" и 4" на большой его оси и по точкам 5' и 6'— вершины 5" и 6" на малой оси.
На рис. 496 рассмотрен случай пересечения наклонного конуса плоскостью, причем последняя задана пересекающимися прямыми АВ и ВС.
Ось родства, определяющая совместно с парой родственных точек, хотя бы А' и А”, родственное соответствие, проходит через точки M1 и М2 пересечения проекций А'В' и А"В", В'С' и В"С". Направление родства перпендикулярно к оси х.
Так как искомое сечение конуса будет находиться в плоскости, определяемой прямыми АВ и ВС, то задача сводится к отысканию на проекциях конуса ряда пар родственных точек в данном родстве.
Строим точку S'1, родственную точке S" (при помощи пары родственных точек D' и D" и точки М3 на оси родства).
Если продолжить фронтальные проекции образующих конуса до пересечения с осью родства в точках N1, N2, N3 и т. д. и затем соединить все эти точки с точкой S'1, прямыми, то определится ряд прямых, расположенных в данной плоскости; проекции этих прямых родственны между собой.
Взяв точку в пересечении горизонтальной проекции образующей с той горизонтальной проекцией S'1N1, S'1N2 и т. д., которая родственна фронтальной проекции этой образующей,
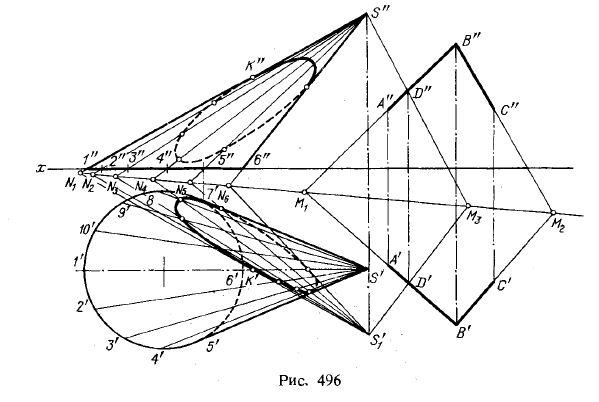
мы получим горизонтальную проекцию точки, принадлежащей фигуре сечения конуса данной плоскостью. Например, точка К' получилась в пересечении прямых S'1N1 и S'1; находим соответственную фронтальную проекцию К". Следовательно, найдена точка К, которая лежит на образующей конуса и в то же время находится в данной плоскости.
Находя подобным способом ряд точек, получаем возможность построить эллипсы, представляющие собой проекции линии сечения.
Вопросы к § 76
- Каковы основные свойства соответствия между двумя пересекающимися плоскостями при параллельном проецировании?
- Как называется такое соответствие?
- Что такое ось и направление родства?
- Какие направления называются главными в данном родственном соответствии?
- Какая фигура родственна окружности?
- Как строятся оси эллипса, родственного заданной окружности, когда направление родства не перпендикулярно к оси родства?
- Как доказать, что между фронтальной и горизонтальной проекциями всякой плоской фигуры существует родственное соответствие?
- В каком случае ось родства фронтальной и горизонтальной проекций плоской фигуры совпадает с осью проекций π2/π1 ?