Пересечение поверхности плоскостью и прямой линией
Решение задач247*. Построить проекции части прямого кругового цилиндра, остающейся после пересечения его фронтально-проецирующей плоскостью Р (рис. 230). Дать натуральный вид сечения и полную развертку поверхности.
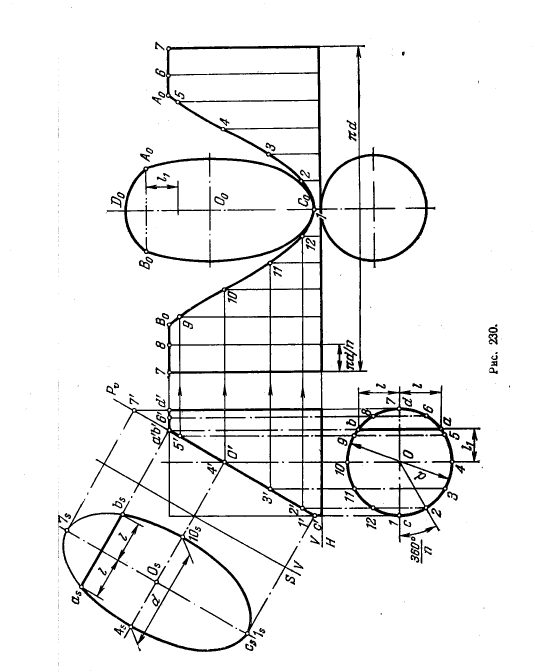
Решение. Судя по положению секущей пл. Р относительно оси цилиндра, линия на его боковой поверхности, получаемая в пл. Р, представляет собой эллипс с центром в О (на оси цилиндра); большая ось эллипса равна отрезку 1'7', а малая — диаметру цилиндра. Учитывая, что пл. Р пересекает и одно из оснований цилиндра, получаем сечение в виде фигуры, ограниченной дугой эллипса и отрезком прямой АВ. Для построения этой фигуры применен способ перемены плоскостей проекций, а именно введена дополнительная пл. S, перпендикулярная к пл. V и параллельная пл. Р. Построение можно было бы осуществить, не вводя пл. S и осей V/H и S/V, а пользуясь большой осью эллипса для откладывания от нее отрезков, взятых на горизонт. проекции, как, например, отрезка l для получения точек аs и bs.
Примененное на рис. 230 деление окружности основания на некоторое число равных между собою дуг (взято 12 дуг) представляет собою обычный прием для построения развертки в подобных случаях. Полная развертка составлена из. а) развертки боковой поверхности, ограниченной пятью отрезками прямой линии и кривой А0С0В0— синусоидой, в которую развернулся эллипс, б) круга основания цилиндра, в) натурального вида сечения, г) сегмента, полученного на верхнем основании.
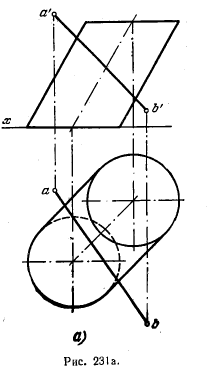
248*. Найти точки пересечения поверхности цилиндра прямой линией (рис. 231, а).
Решение. Применяем для решения задачи общий прием построения точек пересечения прямых линий с любыми поверхностями, а именно: 1) заключение прямой в некоторую плоскость, 2) построение линии пересечения поверхности этой плоскостью, 3) нахождение точки пересечения заданной прямой и этой линии. В данной задаче возьмем вспомогательную плоскость так, чтобы она рассекла поверхность цилиндра по прямым линиям — образующим. Это наиболее простой прием для заданного случая. На рис.231, б показано, что вспомогательная пл. Р определяется прямой АВ и пересекающей ее прямой СМ2, параллельной образующим цилиндра. Такая плоскость рассечет цилиндр по его образующим.
Построение показано на рис. 231, в. Чтобы определить образующие, по которым плоскость, проведенная через АВ, пересечет цилиндр, построены горизонт. следы прямой АВ (точка m'1m1) и прямой СМ2 (точка m'2m2). Через следы прямых проведен горизонт. след плоскости — прямая m1m2 Этот след пересекает в точках 1 и 2 окружность — след цилиндрической поверхности на той же пл. Н. Проведя 1—k и 2—n параллельно сm2, получаем точки k и n — горизонт. проекции искомых точек пересечения АВ с поверхностью цилиндра, а затем k' и n'—фронт. проекции этих точек.
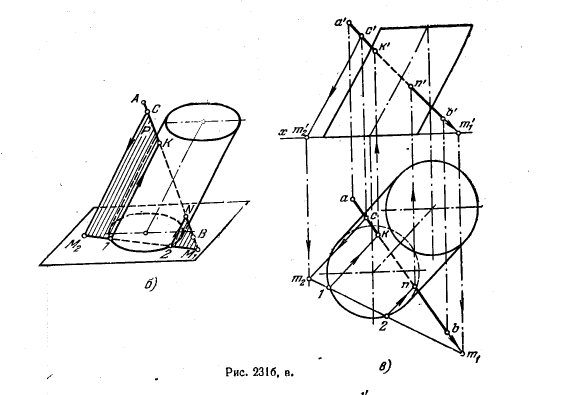
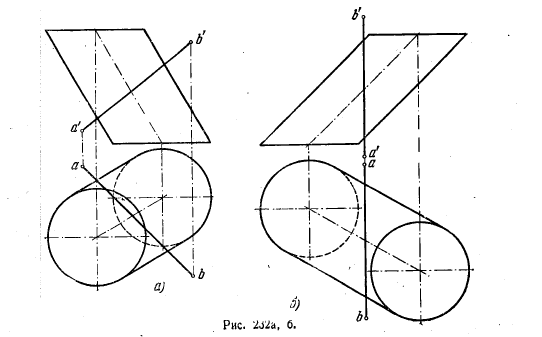
249. Найти точки пересечения поверхности цилиндра прямой линией (рис. 232, а а б).
250*. Построить проекции части прямого кругового конуса, оставшейся после пересечения его фронтально-проецирующей плоскостью (рис. 233, а и б). Дать натуральный вид сечения и полную развертку поверхности изображенного тела.
Решение. Судя по положению секущей плоскости относительно образующих конуса, линия на его боковой поверхности, получаемая в пл. Р, представляет собою эллипс. Большая ось этого эллипса может быть представлена отрезком m'k'. Деля m'k' пополам, получаем фронт. проекцию центра эллипса — точку О', а по ней и проекцию О. Теперь можно найти малую полуось, проведя секущую плоскость
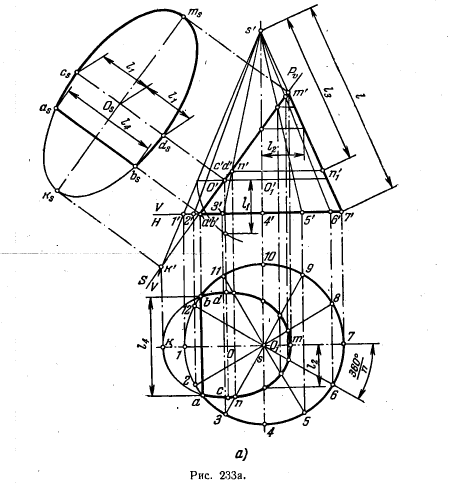
через точку О перпендикулярно к оси конуса и взяв в полученном круговом сечении полухорду l1. Малая ось эллипса равна 2l1 горизонт. проекция эллипса также представляет собою эллипс; его большая ось mk, а малая — cd, равная 2l1.
Последующие построения подобны выполненным на рис. 230. Натуральный вид фигуры сечения построен при помощи способа перемены пл. пр., причем дополнительная пл. S взята совпадающей с пл. Р. Замечание на стр. 187 о том, что построение можно было бы осуществить, не вводя пл. S и осей V/H и S/V, справедливо и для данного случая.
Зная, что боковая поверхность конуса развертывается в круговой сектор с углом φ = d/l · 180° при вершине, где d — диаметр основания, а l — длина образующей конуса, строим сектор с разбивкой его на равные части соответственно разметке
образующих на чертеже конуса. Зная, например, положение образующей S—3 на чертеже и на развертке, находим положение точки N0 на развертке при помощи натуральной величины отрезка l3 образующей от вершины S до точки N.
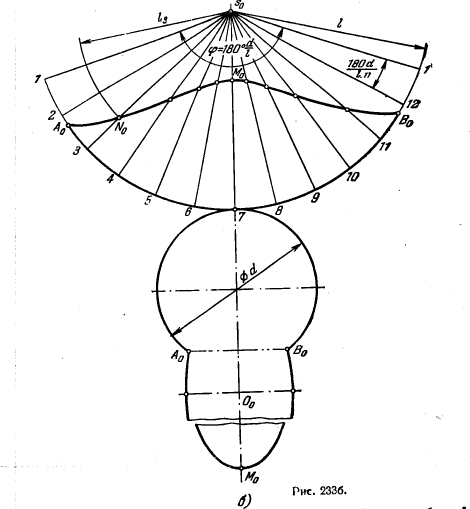
В полную развертку оставшейся части поверхности входят: а) развертка боковой поверхности, ограниченная дугой окружности радиуса l и построенной кривой A0N0M0B0; б) части круга основания, в) натурального вида сечения, причем круг и сечение граничат по хорде А0В0.
251*. Найти точки пересечения поверхности прямого кругового конуса прямой линией (рис. 234, а).
Решение. Применяя вспомогательную плоскость, проведенную через данную прямую линию, задаемся целью обеспечить простейшее пересечение конуса этой плоскостью. Секущую плоскость надо провести через вершину конуса. Она будет пересекать конус по прямым линиям (образующим). На рис. 234, 6 показана пл. Р, проведенная через данную прямую АВ и вершину конуса. Проведя пл, Т,
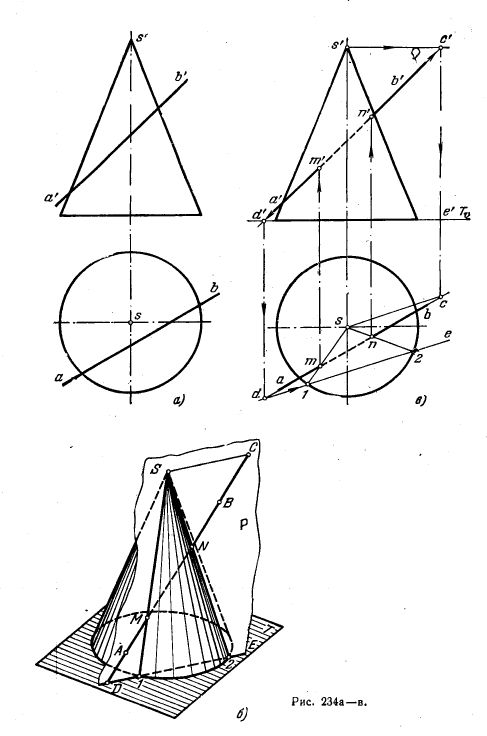
перпендикулярную к оси конуса и, следовательно, пересекающую его по окружности, находим на пл. Т линию ее пересечения с пл. Р — прямую DE. Образующие, по которым пл. Р пересекает конус, определяются вершиной S и точками 1 и 2. На этих образующих и получаются точки К и М, в которых прямая АВ пересекает поверхность конуса.
На рис. 234, в пл. Р задана прямой ЛВ и проведенной через вершину S прямой SC, пересекающей АВ в точке С и параллельной пл. Т. Плоскость Р пересекает пл. Т по прямой DE, параллельной SC. Поэтому, найдя на чертеже точку D (точку пересечения прямой АВ с пл. Т), проводим de || sc. Образующие, по которым пл. Р пересекает поверхность конуса, изображены лишь их проекциями s—1 и s—2. Этого достаточно, чтобы найти горизонт. проекции m и n точек пересечения, а по ним проекции m' и n'.
Если рассматривать конус, поставленный на пл. Н, то надобность в пл. Т отпадает.
252. Найти точки пересечения поверхности конуса прямой линией (рис. 235, а и б).
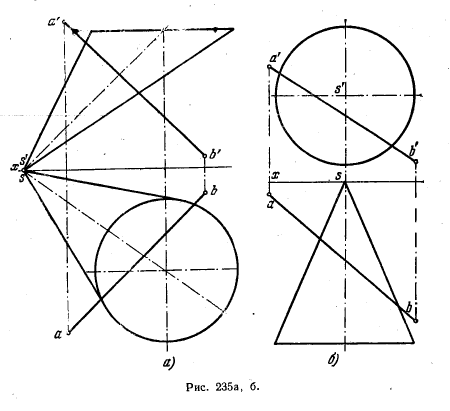
Указание. Принять плоскость круга в качестве вспомогательной плоскости, подобной пл. Т на рис. 234, в.
253*. Найти точки пересечения прямой линии с поверхностью сферы (рис. 236, а).
Решение. Используя вспомогательную секущую плоскость, проходящую через данную прямую (рис. 236, б), получаем окружность. Искомые точки М и N получаются при пересечении этой окружности с прямой линией.
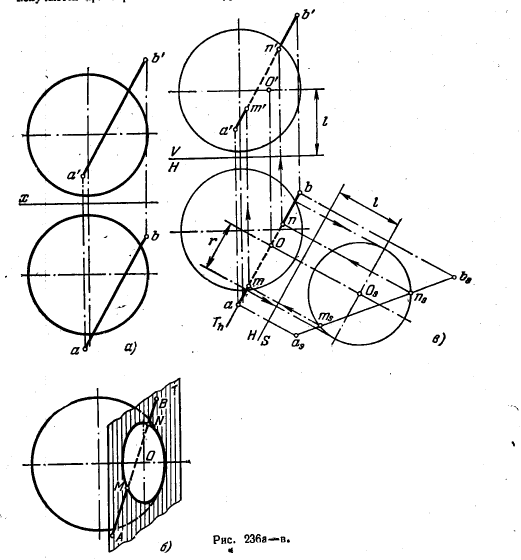
На риc. 236, в показаны графические построения с помощью способа перемены пл. пр.
Дополнительная плоскость S перпендикулярна к пл. H и параллельна вспомогательной горизонтально-проецирующей плоскости Т, проведенной через прямую АВ.
На пл. S изображаем не данную поверхность сферы, а лишь получаемую на ней окружность от пересечения плоскостью Т. Получив также проекцию asbs, находим точки ms и ns, а по ним типи далее m' и n‘.
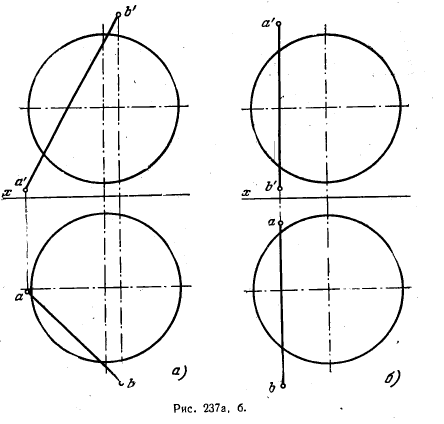
254. Найти точки пересечения прямой линии с поверхностью сферы (рис. 237, а и 6).
255*. Найти точки пересечения прямой линии с поверхностью вращения (рис. 238, а).
Решение. Проводим через прямую АВ (рис. 238-, б) горизонтально-проецирующую плоскость R и строим линию пересечения ею данной поверхности. Точки этой линии находим при помощи параллелей поверхности. Например, проведя дугу Окружности радиуса s—3, получаем на фронт. проекции главного меридиана точку 3'1, определяющую уровень соответствующей параллели, и по точке 3 находим 3'. Точки 4' и 5' получаем по точкам 4 и 5. Высшую точку кривой 1' находим по ее горизонт. рроекции l.
Построив фронт. проекцию кривой, находим точки ее пересечения с фронт. проекцией а'b', а именно точки m' и n' — фронт. проекции искомых точек пересечения прямой АВ с заданной поверхностью. По точкам m' и n' строим m и n.
Если через АВ в качестве вспомогательной плоскости провести фронтально - проецирующую (рис. 238, в), то также придется построить кривую линию. Теперь сначала найдем точки m и n, а по ним m' и n'.
Оба рассмотренных решения по существу друг от друга не отличаются. Но можно представить себе другую схему построения, когда проведение плоскости через
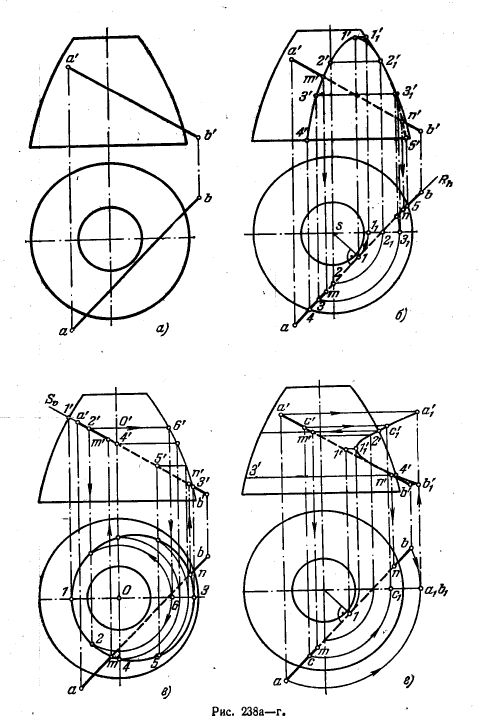
заданную прямую отпадает. Дело в том, что заданная прямая может играть роль образующей однополостного гиперболоида вращения при той же оси, что и у заданной поверхности (рис. 238, а). Так как обе поверхности вращения соосны, то они пересекутся по окружностям. И скомыг точки пересечения прямой с поверхностью вращения получаются на этих окружностях. Предоставляем выполнить такое построение читателю.
Отрицательным моментом в построениях, показанных на рис. 238, б н в, является необходимость пользоваться кривой; это снижает точность определения положения точек М и N. Но и в случае использования гиперболоида вращения приходится строить по крайней мере одну ветвь гиперболы, т. е. опять кривую. Это также снижает качество такого приема решения разобранной задачи
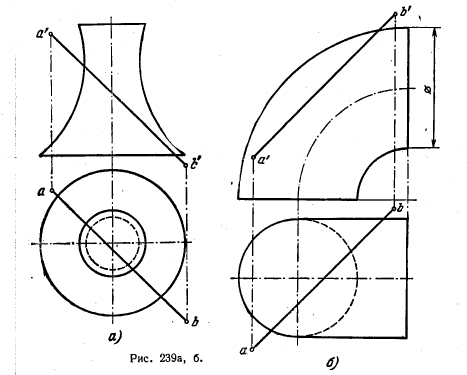
256. Найти точки пересечения прямой линии с поверхностью вращения (рис. 239, а и б).
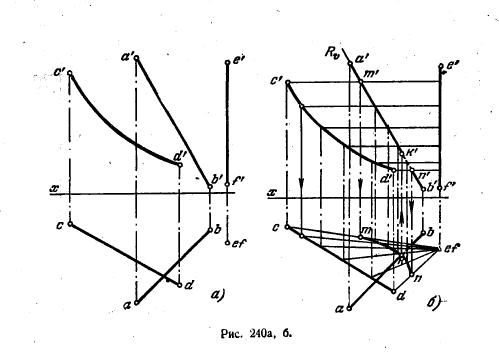
257*. Найти точку пересечения прямой АВ с поверхностью коноида, заданного направляющими CD и EF и плоскостью параллелизма H (рис. 240, а)
Решение. Через прямую АВ (рис. 240, б) проводим фронтально-проецируюшую плоскость R и строим кривую MN пересечения той плоскости с коноидом .Задавая на кривой CD ряд точек, проводим через них образующие параллельно плоскости H; горизонт. проекции этих образующих проходят через точку e(f). Находим точки их пересечения с плоскостью R.
Точка k пересечения кривой mn и прямой ab является горизонт. проекцией искомой точки; по k находим k' на a'b'.
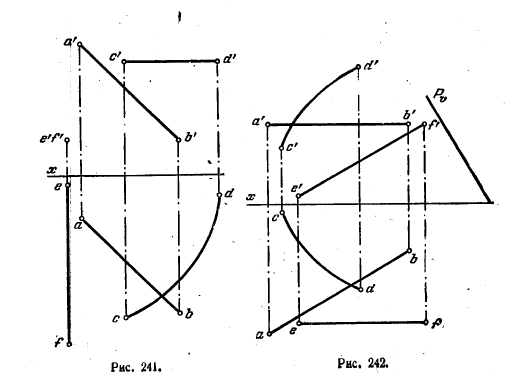
258. Найти точку пересечения прямой АВ с поверхностью коноида, заданного направляющими CD и EF и плоскостью параллелизма V (рис. 241).
259. Найти точку пересечения прямой АВ с поверхностью коноида, заданного направляющими CD и EF и плоскостью параллелизма — фронтально-проецирующей плоскостью Р фис. 242)
260*. Найти точку пересечения прямой АВ (рис. 243, а) с косой плоскостью, заданной направляющими CD и EF и плоскостью параллелизма — фронтально-проецирующей плоскостью Р.
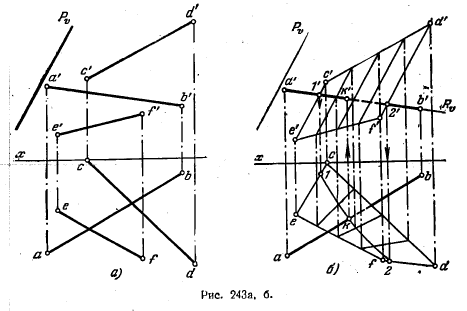
Решение. Через прямую АВ (рис. 243, б) проводим фронтально-проецируюшую плоскость R и находим кривую пересечения ее с заданной поверхюстью .Так же, Как в задаче 257, берем на прямой CD ряд точек, проводим через них образующие (параллельно плоскости параллелизма Р) и строим точки пересечения этих образующих с плоскостью R. Получаем кривую с проекциями 1'2' , 1—2 и точку переселения проекций 1—2 и ab — точку k. Эго горизонт. проекция искомой точки. По k находим k' на а'b'.
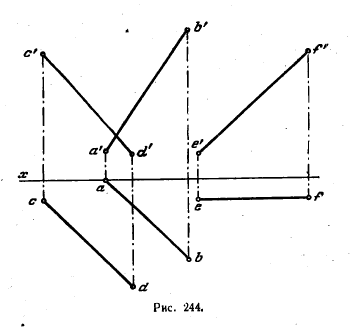
261. Найти точку пересечения прямой АВ с косой плоскостью, Заданной направляющими CD и EF и плоскостью параллелизма Н (рис. 244).
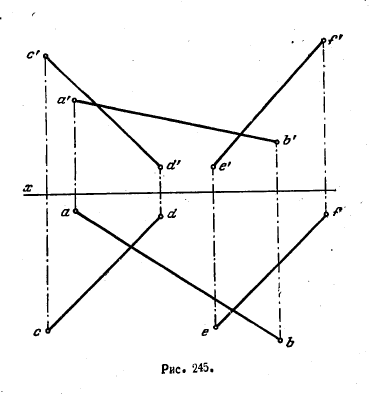
262. Найти точки пересечения прямой АВ с косой плоскостью, (сданной направляющими CD и EF и плоскостью параллелизма V (рис. 245).
263*. а) Разбить поверхность заданного на рис. 246, а тела вращения на зоны различных по своему виду поверхностей; б) построить фронтальную и профильную проекции данного тела вращения, усеченного плоскостями Р1 и Р2.
Решение. Заданное тело вращения состоит из конуса, цилиндра, кругового кольца и сферического сегмента. Соответственно поверхность тела содержит зоны: I—коническую, II— цилиндрическую, III — кругового кольца, IV—сферическую (рис. 246, б).
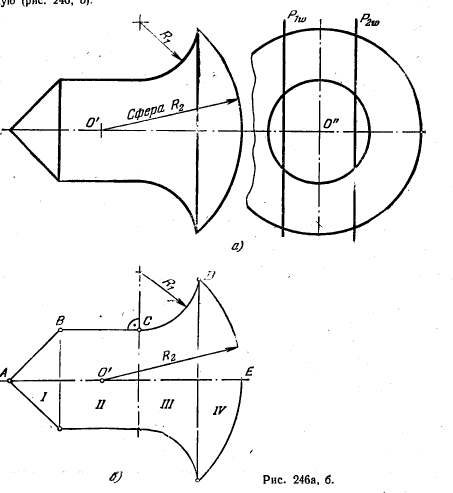
Коническая поверхность образована отрезком АВ, цилиндрическая — отрезкам ВС, поверхность кругового кольца — дугой CD радиуса R1, сферическая — дугой DE радиуса R2.
Каждая из этих зон граничит с соседней по окружности. Окружности проходят соответственно через точки В, С и D.
Плоскость Р2 пересекает (рис. 246, в) коническую поверхность по гиперболе 5-1—4—9, цилиндрическую—по образующим, проходящим через точки 5 и 9, поверхность кругового кольца — по кривой 5—7—8 и сферу — по окружности радиуса R=0'1' . Линии, образуемые на поверхности тела секущей плоскостью Р1, такие же, как от плоскости Р2, и на рис. 246, в их проекции совпадают с построенными, так как плоскости Р2 и Р1 параллельны и отстоят на равные расстояния от плоскости симметрии заданного тела.
Взяв, например, секущую плоскость S1, получаем окружность радиуса 0"3". Эта-окружность дает в пересечении с пл. Р2, точку 4", по которой получаем на фронт. проекции точку 4', принадлежащую гиперболе. Чтобы получить вершину гиперболы, отмечаем точку 1"— профильную проекцию этой вершины — и строим соответствующую ей проекцию 1' на поверхности конуса.
На рис. 246, в показан также пример построения фронт.. проекции одной из точек (7) кривой, по которой пл. Р2 срезает тело в зоне кругового кольца.
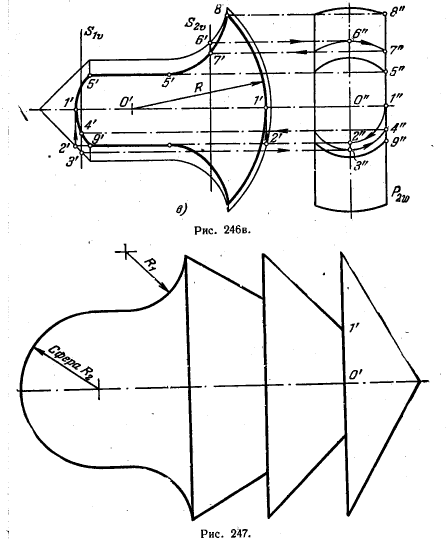
264. Построить линию среза на поверхности тела вращения (рис. 247). Секущую плоскость взять параллельной плоскости проекций У и отстоящей от оси тела вращения на расстояние, равное 1'O' Назвать полученные линии, входящие в состав линии среза.