Общие приемы развертывания гранных поверхностей (призмы и пирамиды)
ТеорияРазвертывание призматической поверхности можно производить по двум схемам. Первая схема (рис. 283):
1) пересечь поверхность плоскостью, перпендикулярной к ребрам;
2) определить длины отрезков ломаной линии, полученной при пересечении поверхности призмы этой плоскостью;
3) развернуть ломаную в прямую A0D0 и на перпендикулярах, проведенных в точках А0, В0, ... к прямой A0D0, отложить длины отрезков ребер А0А, А0А1, В0В, В0В1 и т. д.;
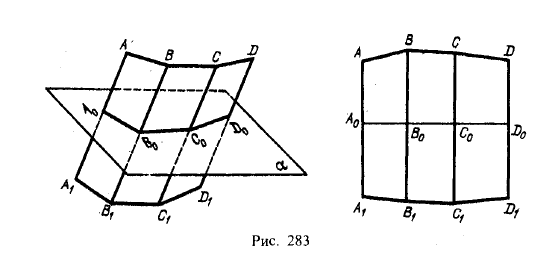
4) провести отрезки АВ, ВС и CD, а также отрезки А1В1, В1С1 и С1D1.
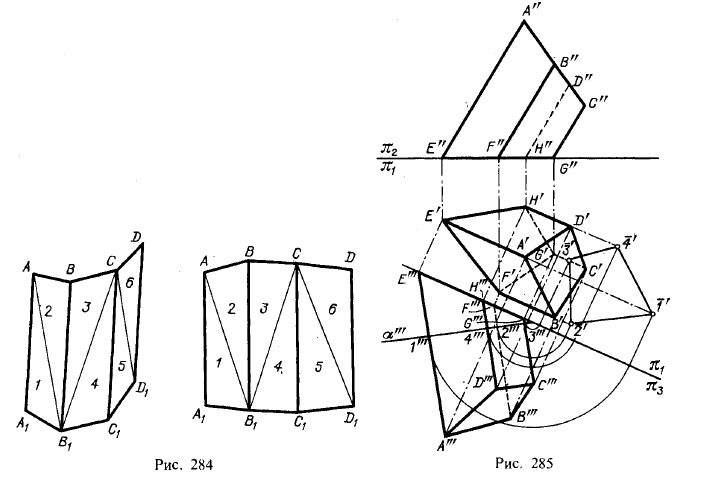
Вторая схема развертывания призматической поверхности заключается в следующем (рис. 284):
1) четырехугольники (грани) разбить диагоналями на треугольники;
2) определить длины сторон этих треугольников;
3) построить последовательно треугольники 1,2,3 и т. д. в плоскости чертежа.
Можно произвести развертывание и так, как указано далее на рис. 287.
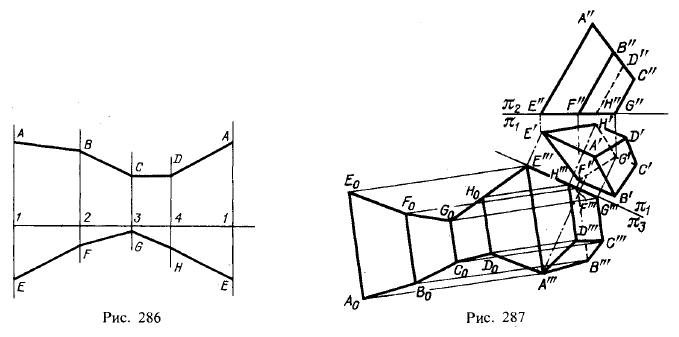
На рис. 285 и 286 дан пример развертывания боковой поверхности призмы.
Построение развертки произведено по первой схеме. На рис. 285 выполнены построениπ1 подготовительные к развертыванию поверхности. Прежде всего, введена дополнительная плоскость проекций π3, перпендикулярная к π1 и параллельная ребрам призмы.
Для получения нормального сечения проведена пл. α, перпендикулярная к ребрам призмы. В системе π3, π1 пл. α перпендикулярна к пл. π3, и поэтому проекция фигуры сечения на пл. π3 находится на следе α"'. Так как пл. α перпендикулярна к ребрам призмы, то проекции этих ребер на пл. π3 перпендикулярны к α'", а так как пл. π3 параллельна ребрам, то их длины равны длинам отрезков А"'Е"', B"'F"' и т. д. Далее, при помощи совмещения пл. α с пл. π1 определяется натуральный вид сечения — четырехугольник 1'2'3'4'.
На рис. 286 показана искомая развертка: на прямой отложены последовательные отрезки 1 — 2 = 1'2', 2 — 3 = 2'3' и т. д., в точках 1,2 и т. д. проведены перпендикуляры к этой прямой, и на них отложены отрезки 1А = 1'"А'", 1Е = 1"'Е"', 2В=2"'В"' и т. д. Затем проведены ломаные ABCDA и EFGHE.
а рис. 287 дано иное построение. Построив проекцию призмы на плоскости π3, параллельной ребрам призмы, проводим из точек Е'", Н'", G'", F"', A'", D'", С"' и В'" прямые, перпендикулярные к Е"'А"'. Из точки Е"' проводим дугу радиуса, равного Е'Н', и в пересечении с прямой, проведенной из точки Н'", получаем точку H0; проводим из нее дугу радиуса, равного H'G', и в пересечении с прямой, проведенной из точки G'", получаем точку G0 и т. д. (G0F0 = G'F', F0E0 = F'E'). Из точек Н0, G0, F0, Е0 проводим прямые параллельно Е"'А"' до пересечения с соответствующими прямыми, проведенными из точек D"', С"', В"' и А'". Указанный вариант целесообразен, когда величина сторон основания может непосредственно взята с чертежа.
Развертывание боковой поверхности пирамиды можно производить по следующей схеме:
1) определить длины ребер и сторон основания пирамиды;
2)построить в плоскости чертежа последовательно треугольники — грани пирамиды.
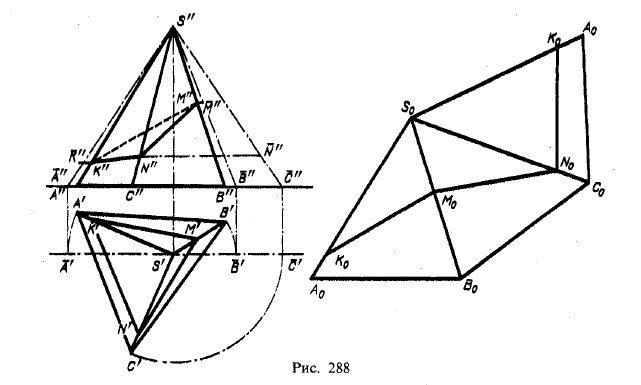
На рис. 288 выполнено построение развертки боковой поверхности пирамиды с нанесенными на ее грани сторонами треугольного сечения пирамиды некоторой плоскостью. Найдена длина каждого из ребер, затем построен треугольник A0S0B0 по трем сторонам: основание А0В0 взято равным горизонтальной проекции А'В', а боковые стороны взяты равными натуральным величинам ребер SA и SB (т. е. отрезкам S"A" и S"B").
Далее, на стороне S0B0 построен второй треугольник, причем две другие стороны взяты следующих размеров: сторона В0С0 равна горизонтальной проекции В'С', сторона S0C0 равна длине ребра SC (т. е. отрезку S"C").
Так же построен и третий треугольник. В результате получена развернутая боковая поверхность пирамиды. Если теперь на сторонах S0A0, S0B0 и S0C0 отложить отрезки S0K0, S0M0 и S0N0, равные отрезкам ребер пирамиды, пересеченной плоскостью, то получим ломаную линию K0M0N0K0, состоящую из сторон фигуры сечения.
Вопросы к §§ §§ 43-44
- Как строится линия пересечения одной гранной поверхности другой?
- В каком случае целесообразно применять плоскости общего положения (как вспомогательные) при взаимном пересечении двух пирамид и как проводить эти плоскости?
- По каким схемам можно производить развертывание поверхностей, ограничивающих призмы и пирамиды?
- В каком случае эти развертки будут полными?